| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
ANAMORPHOSE EN 3D
3D
Anamorphosis
| Du grec ana "en remontant, qui marque le retour vers", et morphe "forme". |
Le terme anamorphose désigne d’une façon
générale, la transformation qui à un objet fait correspondre
l'objet dont il est l'image virtuelle dans un système optique, pour
un observateur donné situé à distance finie ou infinie.
| Dans l'espace, nous définirons l'anamorphose
associée à une surface |
 |
| On obtient les coordonnées de M' par la
relation |
Cette relation transforme une courbe
en une courbe
,
dite anamorphose de la première.
Exemples :
- une anamorphose plane (
= plan) n'est autre qu'une réflexion.
- anamorphose sphérique :
|
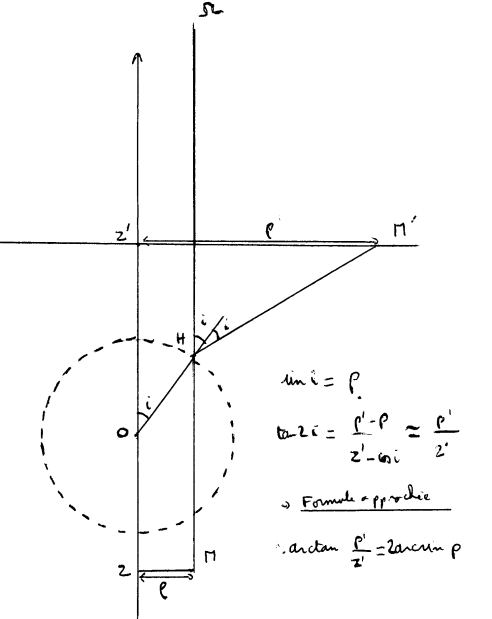
Ici, l'observateur est à l'infini dans la direction de Oz, et M(x, y, z), M'(x', y', z') : on a (donc
|
 |
  |
Vue d'une anamorphose sphérique pour un observateur
situé à l'infini dans la direction de Oz, avec transformation
d'un quadrillage et d'une courbe.
Le quadrillage en dôme est le quadrillage réel dont l'image virtuelle pour un observateur situé sur Oz à l'infini est le quadrillage plan. |
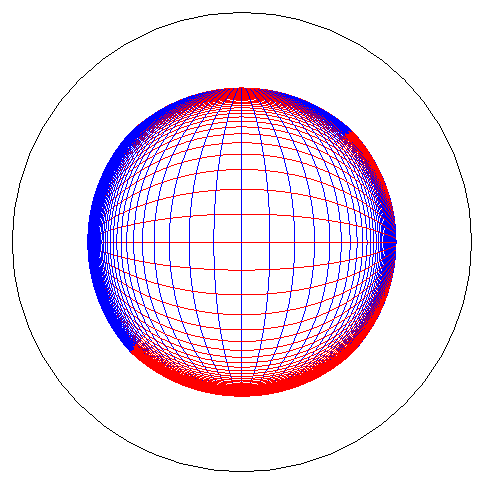
Image obtenue en utilisant la formule approchée ci-dessus |
Image réfléchie par la sphère d'un
quadrillage placé dans le plan z = 1, pour un observateur
situé à l'infini dans la direction de Oz.
Le rayon de la boule interne vaut 1/
|
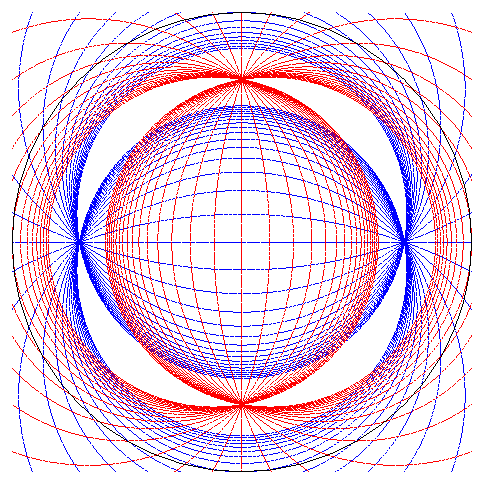 |
Image réfléchie par la demi-sphère z < 0 d'un quadrillage placé dans le plan z = 0. |
Résultat réel :
|
|
 |
voir aussi :
melusine.eu.org/syracuse/mluque/BouleMiroir/boulemiroir.html
- anamorphose cylindrique : voir la
page sur le cas
plan ; les formules de transformation pour le cylindre
et un observateur à l'infini dans la direction de Oy sont
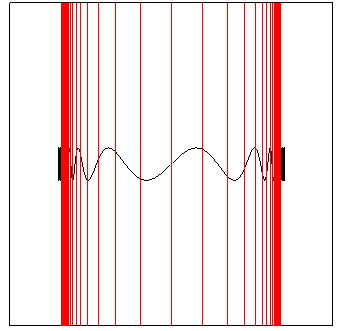
| Image réfléchie par le cylindre |
 |
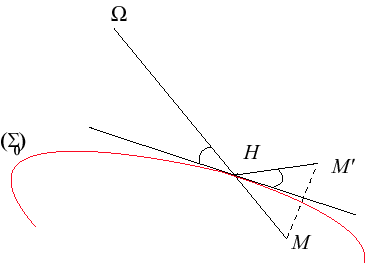
- Anamorphose conique :
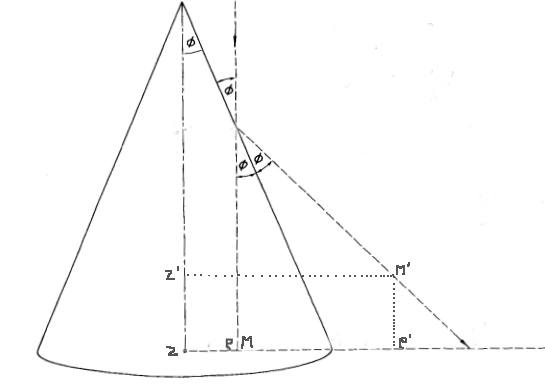
| Lorsque l'observateur est à l'infini dans la direction
de l'axe du cône, l'anamorphose est la transformation qui dans tout
plan passant par l'axe du cône se réduit à la symétrie
par rapport à la génératrice correspondante (voir
figure).
Si On en tire |
 |
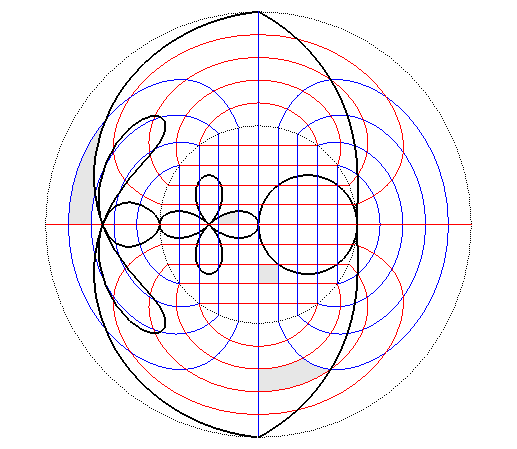 |
Vue d'une anamorphose conique pour un observateur situé
à l'infini dans la direction de Oz, avec transformation d'un
quadrillage et d'une courbe.
Le quadrillage image est formé de portions de conchoïdes de droites, et l'image du cercle noir est une portion de conchoïde de cercle, ou limaçon de Pascal.  |
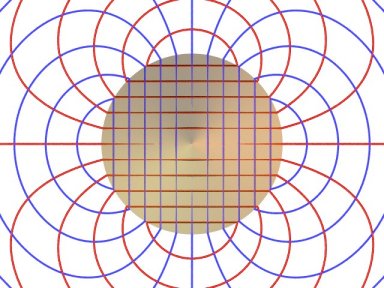
Vue du reflet d'un réseau de conchoïdes de Nicomède (réalisée par alain Esculier avec povray) |
 Les courbes reflétées sont de nouveau des portions de conchoïdes de Nicomède. |
Pour certains auteurs, le terme d'anamorphose désigne
plus simplement la transformation qui à un objet fait correspondre
son symétrique par rapport à un miroir courbe.
| Dans l'espace, l'anamorphose (au sens n°2)
associée à une surface |
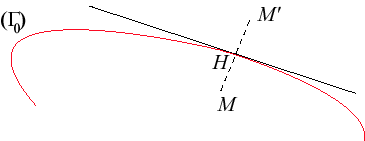 |
Contrairement à l'anamorphose vue précédemment, cette relation est symétrique.
Quelques images réalisées par Alain Esculier :
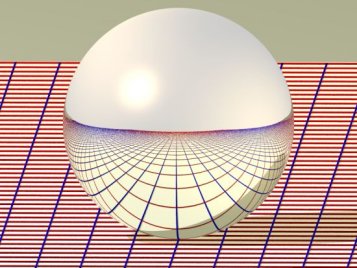
Anamorphose sphérique convexe |
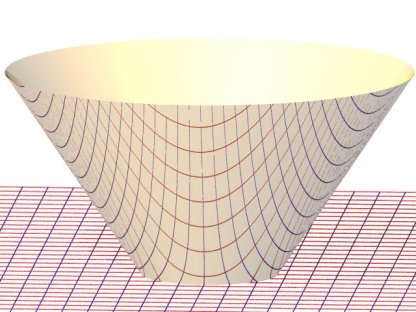
Anamorphose conique |

Anamorphose cylindrique concave ; ce miroir concave inversant droite-gauche, l'écriture est dans le bon sens dans le miroir contrairement à un miroir plan ! |

Anamorphose sphérique concave : il y a inversion droite-gauche et haut-bas. |

M.C. Escher Main tenant un miroir sphérique 1935 |

M.C. Escher
|



Les miroirs déformants du jardin d'acclimatation.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2004