| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
3D ANAMORPHOSIS
| From the Greek ana "going up, going back", and morphe "shape". |
The word anamorphosis refers, in a general fashion,
to the transformation that maps an object onto the object of which it is
the virtual image by an optical system, for a given viewer at finite or
infinite distance.
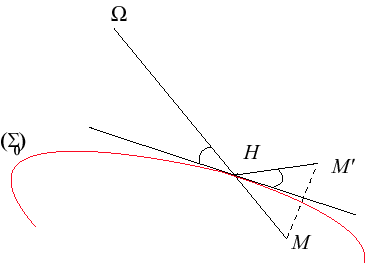
| In space, define the anamorphosis associated to
a surface |
 |
| The relation |
This relation transforms a curve
into a curve
,
said to be an anamorphosis of the former.
Examples:
- a plane anamorphosis (
= plane) is none other than a reflection.
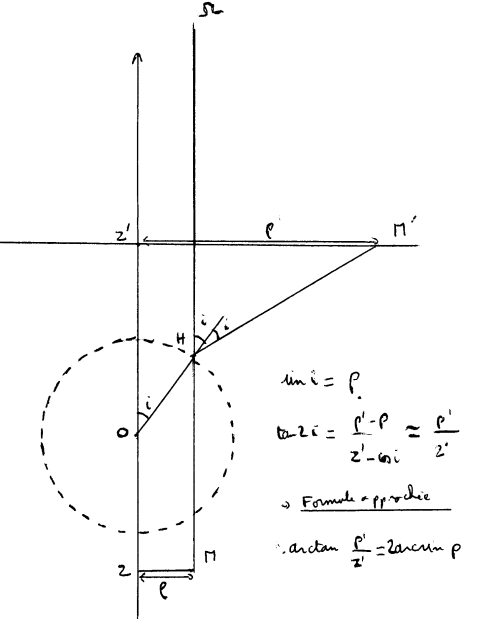
- spherical anamorphosis:
|
Here, the observer is at infinity in the direction of Oz, and M(x, y, z), M'(x', y', z'): we have (therefore,
|
 |
  |
View of a spherical anamorphosis for an observer located
at infinity in the direction of Oz, along with the transformation
of a grid pattern and a line.
The dome-like grid pattern is the real grid pattern the virtual image of which is, for an observer located on Oz at infinity, the planar grid pattern. |
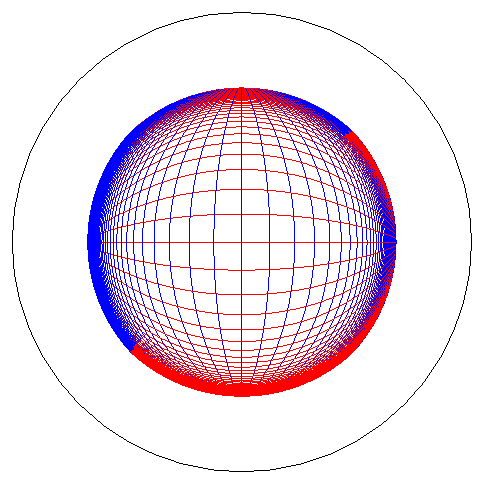
Image obtained by using the approximate formula above |
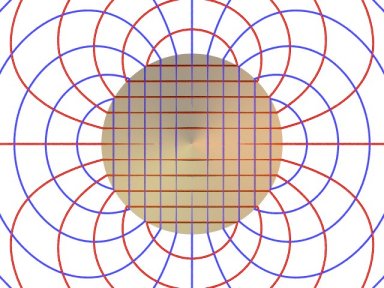
Image of a grid pattern placed on the plane z
= 1, reflected by the sphere, for an observer located at infinity in the
direction of Oz.
The radius of the internal ball is equal to 1/
|
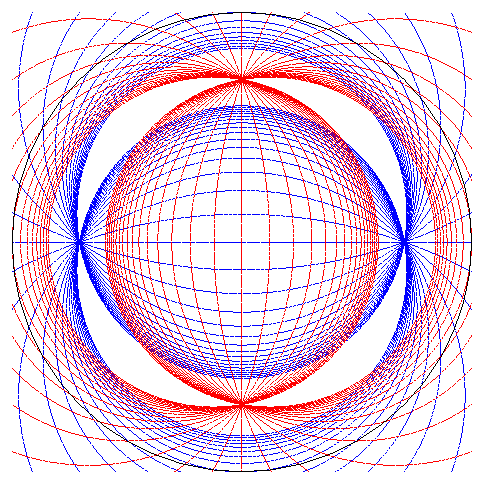 |
Image of a grid pattern placed on the plane z = 0 reflected by the half-sphere z < 0. |
Real result:
|
|
 |
See also:
melusine.eu.org/syracuse/mluque/BouleMiroir/boulemiroir.html
- cylindrical anamorphosis: see the
page dedicated to the
planar case; the transformation formulas for the cylinder
and an observer at infinity in the direction of Oy are
| Image of vertical lines and a sinusoid placed on the
plane y = - 1 reflected by the cylinder |
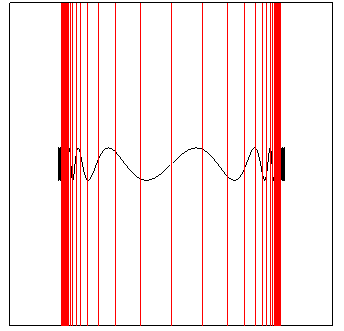 |
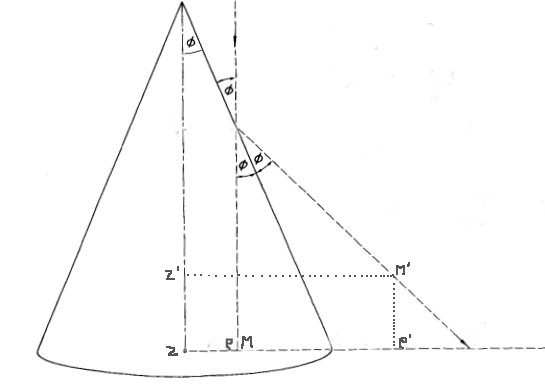
- conical anamorphosis:
| When the observer is at infinity in the direction of
the axis of the cone, the anamorphosis is the transformation that amounts,
in any plane passing by the axis of the cone, to the symmetry with respect
to the corresponding generatrix (see figure).
If We derive from this |
 |
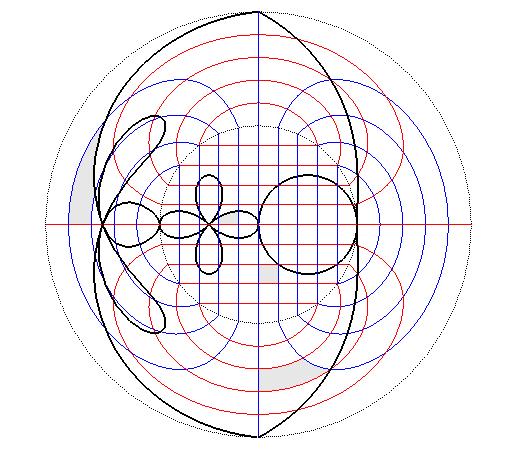 |
View of a conical anamorphosis for an observer located
at infinity in the direction of Oz, along with the transformation
of a grid pattern and a curve.
The image of the grid pattern is composed of portions of conchoids of Nicomedes, and the image of the black circle is a portion of the conchoid of a circle, or limaçon of Pascal.  |
View of the reflection of a lattice of conchoid of Nicomedes (made by Alain Esculier using povray) |

Inverse transformation of an exterior grid pattern. The reflections are, again, portions of conchoids of Nicomedes. |
For some authors, the word anamorphosis refers more simply
to the transformation that maps an object onto its symmetrical image with
respect to a curved mirror.
| In space, the anamorphosis (in the second sense)
associated to a surface |
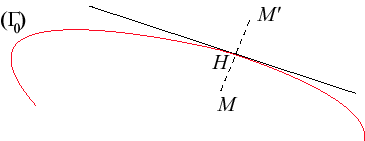 |
As opposed to the previous anamorphosis, this relation is symmetrical.
Some images made by Alain Esculier:
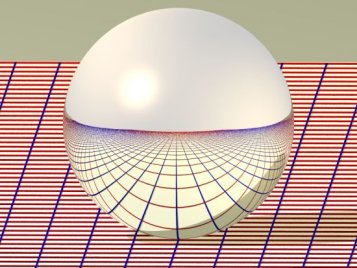
Convex spherical anamorphosis |
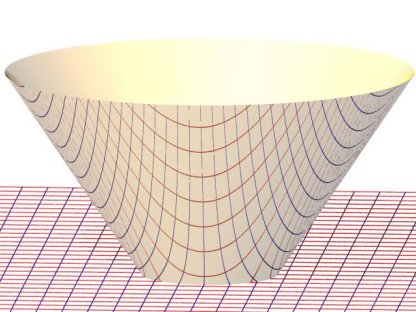
Conical anamorphosis |

Concave cylindrical anamorphosis; this concave mirror switches right and left, so the writing is not reversed on the mirror, contrary to what happens with a planar mirror! |

Concave spherical anamorphosis: left and right as well as up and down are switched. |

M.C. Escher Hand with Reflecting Sphere 1935 |

M.C. Escher
|



The distorting mirrors in the Jardin d'acclimatation, Paris.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018