Anamorphosis

ANAMORPHOSIS

Process studied by Jean-François Nicéron in 1636.
From greek ana "going up", or going "back to", and morphe "form".

The word anamorphosis commonly refers to the transformation that matches an object with the one which it is the virtual picture through an optical system, for a given viewer from a finite or infinite distance.

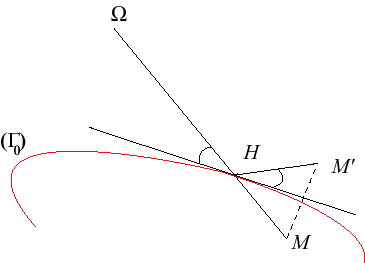
In two-dimensional space, the anamorphosis associated with a curve (the mirror) and a point (the viewer) can be defined as the relation that matches any point with its mirror-symmetrical image(s) starting from , i.e. any point M' symmetrical of M with respect to the tangent in H of , H being the intersecting point of the line (M) and the mirror ; so that a light ray coming from M' reaches the viewer's eye after a reflexion at H and M is a virtual image of M'. Clearly, the viewer thinks he sees M, meanwhile he's actually seeing M'.

Coordinates of M' are determined by the relation where is the normal vector of at H ;
For example, if is the trigonometric circle and the viewer stands at infinity in the direction of Oy, and M(x, y), M'(x',y'), we get with and u = x (then ), we finally get (see figure below).
For a curve with the complex parametrization u(t), and a viewer at infinity in the direction of Oy, the relationship between M(z) and M'(z') is obtained by eliminating t in the following relations .

That relation turns a curve into a curve , obtained by anamorphosis of the first one.

Examples :

- a rectilinear anomorphosis ( = line) is nothing but a reflection.

- a circular anamorphosis :

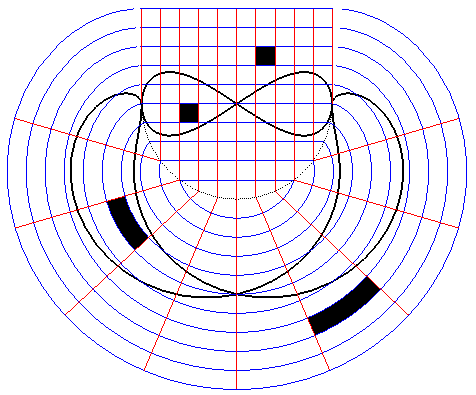Image of a circular anamorphosis as viewed from an observer at infinity in the direction of Oy, with transformation of a grid and a curve.
The curved grid is the real grid whose virtual image is the original grid.

The bidimensional circular anamorphosis is similar to the planar restriction of the tridimensional cylindrical anamorphosis, as shown in this picture.

Conversely, here is the virtual image of a real grid (this implies reversing the relation )

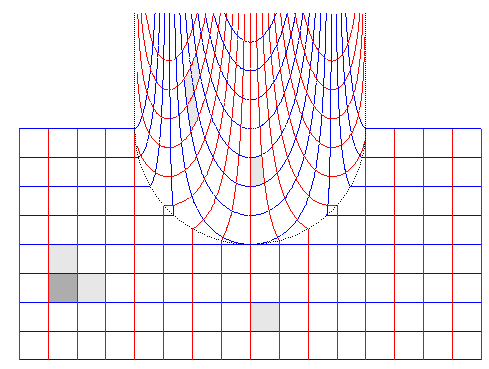Cylindrical anamorphosis obtained with Povray software (Alain Esculier)

For some writers, the word anamorphosis simply describes the transformation that matches an object with its symmetrical image with respect to a curved mirror.

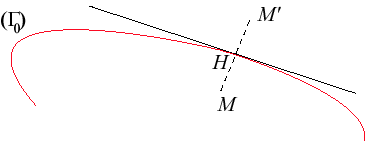In the plane, the anamorphosis (second meaning) associated with a curve (the mirror) is the relation that matches every point M to its symmetrical image(s) with respect to the mirror, i.e. every point M' symmetrical image of M with respect to an orthogonal projection H of M upon .

As opposed to the previously seen anamorphosis, this relation is symmetric.

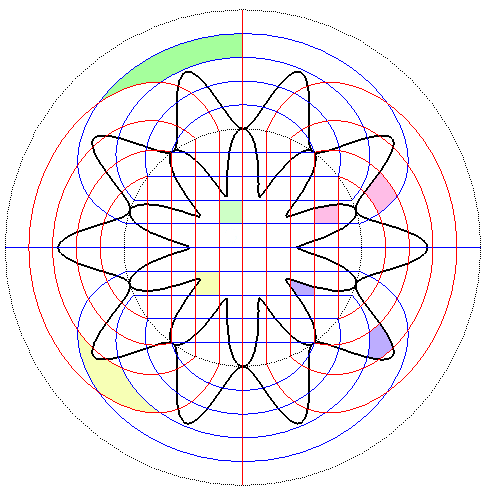View of a circular anamorphosis (second definition) transforming a grid and a curve.
For a circular mirror of radius a centered on O, the transformation formulas in polar coordinates are .
The blue and red curves are quartics.