Anguinea

ANGUINEA

Curve studied by L'Hospital and Huygens in 1692, then by Newton in 1701.
From the Latin anguis "snake, hydra, dragon" (your choice !), name given by Newton.
Other name : serpentine cubic.

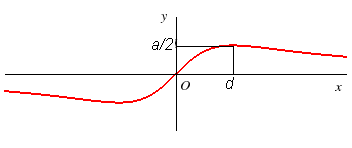Cartesian equation: .
Cartesian parametrization:.
Rational cubic with isolated point (at infinity in the direction of Oy).
Polar equation: .

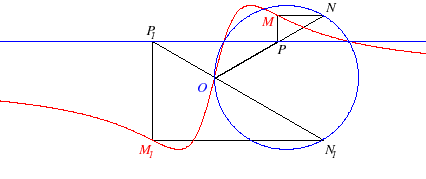
The anguinea is the hyperbolism of the circle with respect to a point O of this circle and a straight line parallel to the diameter passing through O.
Here, the circle is the circle of diameter [OA] with A(a, 0) and the line, y = d.

Like the witch of Agnesi, it is a projection of the horopter.

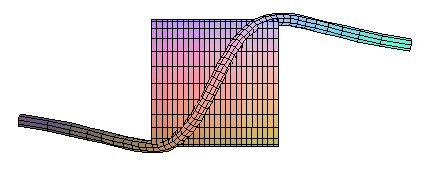To bring back the isolated point at infinty to a finite distance, we can use the homographic transformation : that transforms the anguinea into the mixed cubic : having its isolated point in O.

In the figure hereafter, we used instead of for more readibility.

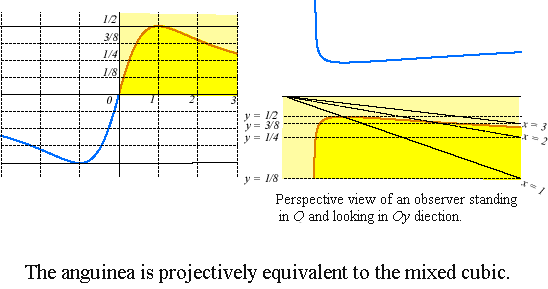
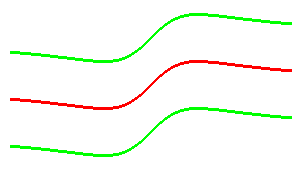
The anguinea is a directrix curve of the Plücker's conoid.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

The anguinea is the hyperbolism of the circle with respect to a point O of this circle and a straight line parallel to the diameter passing through O. Here, the circle is the circle of diameter [OA] with A(a, 0) and the line, y = d.
Like the witch of Agnesi, it is a projection of the horopter.