| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
ANTICAUSTIC
| Notion studied by Quételet
in 1825 and Mannheim
in 1861.
Other name: secondary caustic (given by Quételet). Be aware that the word anticaustic is sometimes also given to the notion named in this website as "inverse caustic". |
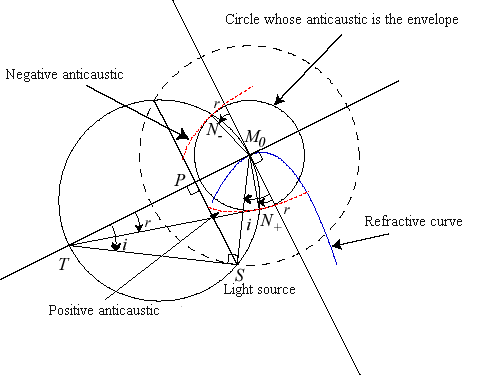
The anticaustic (by refraction) of a curve 
(the refracting curve), with respect to a point S, and associated
with a constant value n > 0 is the envelope of a circle (C)
centered on M0 on
and with a radius of 
; that is to say, the radius stays in a constant ratio with the distance
of M0 to the
light source.
Its name comes from the fact that this curve is used to
determine the
complete caustic by refraction
of for
S
and n (n is the ratio 
of the refraction indices on S's side and on the other side, therefore
it's also the ratio of the speeds of light on each side) ; the caustic
is indeed the evolute of the anticaustic.
| The feature points of the circle (C),
M+
on S side and M-
on the other, are the intersection points of (C) with the circle
with a diameter of [M0T],
where T is the intersection point of the tangent (T0)
on M0 of (G0)
with the normal at S of the incident ray (SM0).
Here, 
where i is the angle with the normal of the incident ray, r
is the angle with the refracted ray ; hence  .
M+ describes the positive anticaustic, whose evolute is the caustic by refraction associated with the constant value +n ; and M- describes the negative anticaustic, whose evolute is the caustic by refraction associated with the constant value-n. |
 |
When n = 1, the anticaustic is the orthotomic
curve, and the caustic is then the caustic by reflection.
Anticaustics of straight lines are conics.
More precisely, if S' is the symmetric of S
with respect to a line (D), the anticaustic of (D) with respect
to S for the constant value n is
- the ellipse of focal points S
and
S' and of eccentricity n such that 
if n < 1.
 |
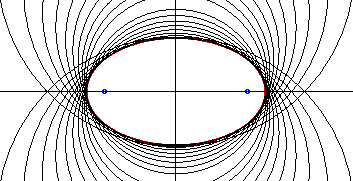The ellipse is the envelope of the circles centered on
its non focal axis and having a radius equal to the ratio of the distance
from the center to the focal point and the eccentricity of the ellipse.
The positive anticaustic is the part situated on the side of S with respect to (D) and the negative anticaustic is the other part. |
- the hyperbola of focal points S
and
S' and of eccentricity n such that 
if n > 1.
 |
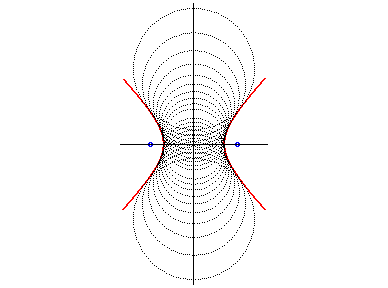The hyperbola is the envelope of the circles centered
on its non-focal axis and having a radius equal to the ratio of the distance
from the center to the focal point and the eccentricity of the hyperbola.
>The positive anticaustic is the branch situated on the side of S, and the negative anticaustic is the other branch. |
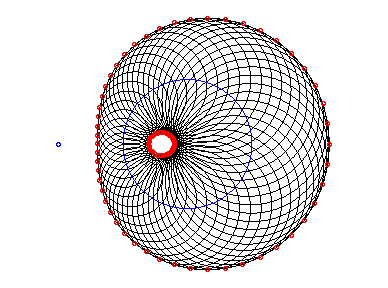
Anticaustics of circles are Cartesian ovals (including Pascal's snails, obtained when the light source is on the circle).
More precisely, if S' is the conjugate of
S
with respect to a circle (C) with center O having a radius
R,
the anticaustic of (C) with respect to S for the constant
value n is the Cartesian oval : 
, where; 
.
Anticaustics have two beautiful reciprocal properties, forming Mannheim's
theorems :
1) the inverse of the anticaustic is the anticaustic of the inverse.
2) the anticaustic of the anticaustic (with the same index n
and with respect to the same light source F) is a curve similar
to the starting curve (center F and ratio 1-1/n2).
Examples of application: the caustic by complete refraction of a Cartesian
oval with respect to a focal point bring another focal point, the anticaustic
is a circle. Anticaustics of circles are then Cartesian ovals.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017