| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
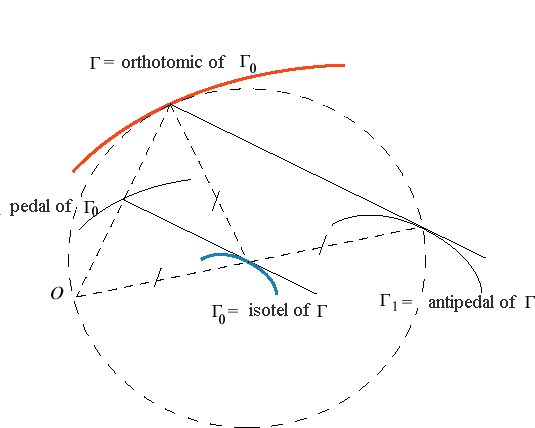
ORTHOTOMIC CURVE
| Notion studied by Quételet in 1822 (?)
From the Greek orthos "right" and tomê "to cleave". Other name: podoid. |
The orthotomic of a plane curve 
with respect to a point O is the locus of the symmetric images of
O
about the tangents to the curve .
It is therefore the image of the pedal
of with
respect to O by a homothety with centre O and ratio 2.
It is also the envelope of circles centred on, and passing by, O; see anallagmatic curve. |
 |
Its evolute
is the caustic by reflection of
for a light source placed at O: the orthotomic curve is therefore
also a special case of anticaustic
(or secondary caustic).
The orthotomic curve can also be considered as a roulette:
when the curve
rolls without slipping on itself in such a way that the two curves are
symmetric images of one another about their common tangent, the trace of
the point O of the moving plane on the fixed plane is the orthotomic
curve (this is why, for example, the cardioid
is, at the same time, the pedal of a circle with respect to one of its
point and an epicycloid. See also the construction of the cissoid
of Diocles as a roulette).
Examples:
- the orthotomic of a centred conic
with respect to one of its foci is the directrix circle centred on the
other focus;
- the orthotomic of a parabola
with respect to its focus is its directrix.
For exhaustive examples; see pedal.
The curve of which a given curve is the orthotomic is the isotel of the initial curve.
See also the notion of symmetric
image of a curve
about ,
which gives the orthotomic when
is reduced to a point.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017