| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
| Curve studied by Rømer in 1674, Vaumesle in 1678,
La Hire in 1708 and Castillon in 1741.
The name, given by Castillon in 1741, comes from the Greek kardia "heart". |
 |
Polar equation: 
Cartesian equation:  .
Rational bicircular quartic. Cartesian parametrization: 
(where  ).
Rational Cartesian parametrization:  .
Complex parametrization:  (where ).
Polar, cartesian tangential angles:  , .
Curvilinear abscissa: 
Radius of curvature: 
Intrinsic equation 1: 
Intrinsic equation 2:  (here,
cte=
- )
Pedal equation: 
Length: 8 a ; area: 3pa2/2. |
The cardioid and Bernoulli's lemniscate are in a contest for the record of the number of different families of remarkable curves they belong to.
The cardioid is indeed:
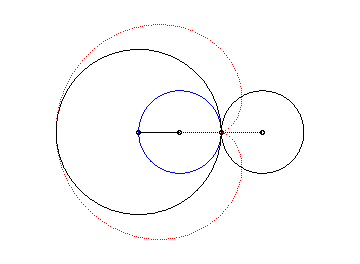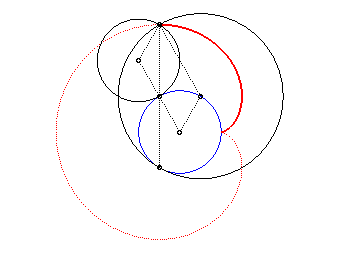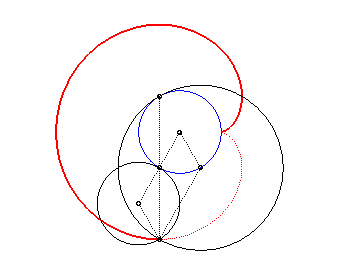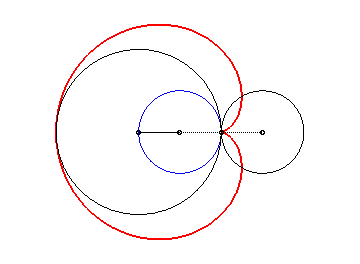
1) the conchoid
of a circle with respect to a point located on the circle and a modulus
equal to the diameter of the circle. To find the equation written in the
header, take the conchoid of the circle (C), centred in W
(a/2, 0) passing through O, with respect to O and
modulus a (therefore, the cardioid is a special case of Pascal's
limaçon). We thus deduce the construction below based on a stick
of length 2a sliding through a fixed point on (C) and whose
centre is constrained to describe (C).
 |
 |
2. a) an epicycloid with one cusp: the locus of a point on a circle rolling externally without slipping around a circle of equal radius (here circle of radius a/2 rolling without slipping around the circle (C)).
 |
 |
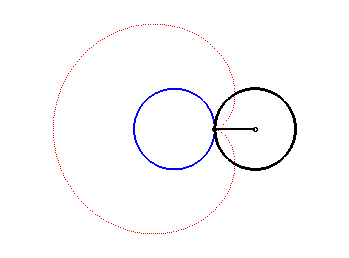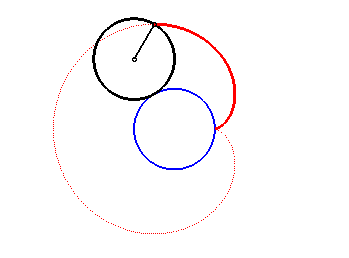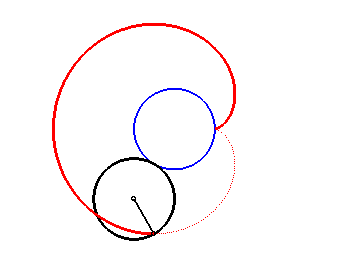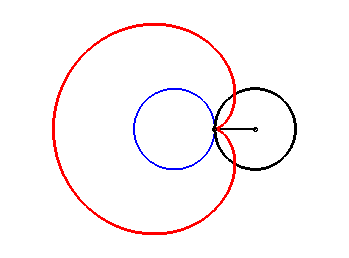
d) the envelope of a diameter of a
circle of radius a rolling externally without slipping on (C0).
e) the envelope of a chord (PQ)
of the circle of centre W and radius 
(circumscribed
circle of the cardioid), P and Q describing this circle in
the same direction, one of them going twice as fast as the other (generation
said to be "of Cremona").
Above, the point n is linked to the point 2n modulo 30. |
 |
3) as are all rational
bicircular quartics:
3. a) the pedal
of a circle with respect to one of its points ; here, the pedal of
the circle (C') of centre (a, 0) passing through O
with respect to O ((C') is the inscribed circle of the cardioid).
3. b) therefore the cardioid also is the envelope of the circles for which a diameter joins a fixed point (here O) on a circle (here the circle (C'), in red below) and another point on this circle.
The blue circle above is the circle formed by the centres of the family of circles. It is in fact the initial curve of this cyclic generation.
3. c) the inverse
of a parabola with respect to its focus (here the equation of the parabola
being 
,
the focus being O).
3. d) the cissoid of two tangent circles, the second's radius being twice the first's, with respect to the centre of the big one (here cissoid with respect to O of the circle of centre (a/2, 0) passing by O and the circle of centre O and radius a - this definition is in fact equivalent to the definition in terms of conchoid).
4) the caustic,
by reflection, of a circle, with a light source located on the circle
(here the circle of centre (3a/2, 0) passing through O).
 |
 |
The cardioid appears in this conical container full of milk thanks to this property (see caustic surface):
5) the orthocaustic of a trisector limaçon with respect to the summit of its loop.
6) the orthocaustic of Cayley's sextic with respect to the summit of its loop.
7) the pedal of a right cissoid with respect to the point (4a, 0).
8) a special case of sinusoidal spiral.
9) a glissette: the cardioid is the locus of the vertex of a variable parabola with fixed focus and passing through a fixed point.
10) the complex field lines defined by 
are cardioids.
| Like for all cycloidal curves, the evolute of the cardioid is a similar cardioid, image of the initial one by the homothety of centre W and ratio –1/3. |
 |
| Thus one of the involutes is also a cardioid ; the other ones are self-parallel curves (animation of the construction of one of them opposite). |
 |
|
The parametrization of the parallel curve at distance d is  .
Thanks to the cuspidal point, it is itself parallel to itself at distance
–d, hence self-parallel.
The cusps do travel along the whole evolute. |
 |
| The roulette of the cusp of the cardioid rolling on a cycloid of equal length is linear: |  |
The orthoptic of the cardioid is composed of a circle and a Pascal's limaçon.
The cardioid also appears in some spherical cycloids and in multicardioids.
Finally, a beautiful cardioid can be found in the middle of Mandelbrot's set:
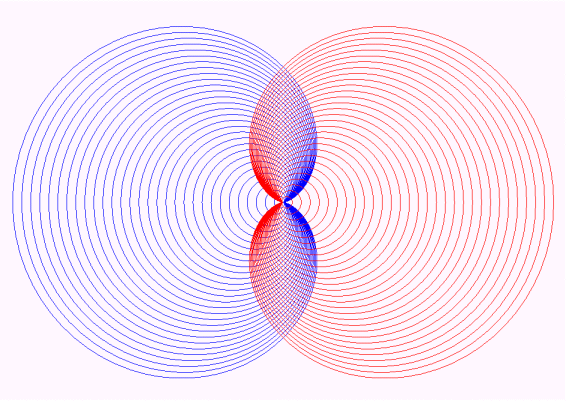
The cardioids r = a
(1 + cosq)
for a > 0 and their symmetrical image about Oy form an orthogonal
lattice.
|
 The curves of equation |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
(
(Thierry LEGAY's idea).