GLISSETTE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
GLISSETTE

| Notion studied by Catalan in 1865 and by Besant
in 1869.
See [Brocard]. |
| The glissettes are curved traced on a fixed plane
by a point on a moving plane, the motion of the moving plane being described
by the movement of two of its curves sliding on two curves of the fixed
plane.
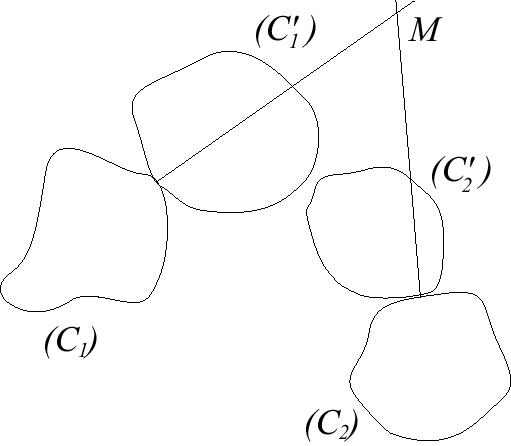
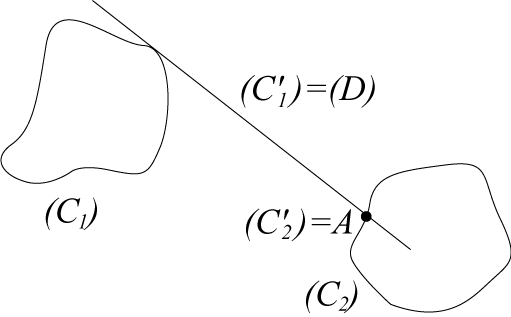
More precisely, let (C1) and (C2) be two curves of a fixed plane (the bases), and (C'1) and (C'2) two curves of the moving plane (the sliding curves): the motion of the moving plane is determined by the fact that (C'1) stays tangent to (C1) and (C'2) to (C2). The associated glissettes are the traces of a point of the moving plane on the fixed plane. Note that since all motions
of a plane over a fixed plane are described by a rolling curve rolling
on a base, any glissette is in fact also a roulette.
From this we derive a beautiful duality theorem: if the
bases and sliding curves are swapped (i.e., (C'1)
and (C'2) are fixed and (C1)
and (C2), respectively, slide over
them), then the base and the rolling curve of the motion of a plane over
a fixed plane are also swapped.
|
 |
SPECIAL CASE N° 1 (original case, that gave rise to the notion of glissette)
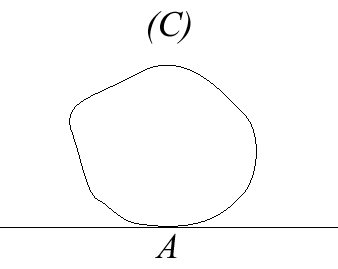
| Case where (C1)
is a line (D), (C2) is reduced
to a point A on the line (D), and (C'1)
and (C'2) coincide (and we write
them (C)); the motion of the moving plane is therefore defined by
the fact that the sliding curve (C) stays tangent to the line (D)
at the point A.
The instant centre of rotation of this movement of a plane over a fixed plane is the centre of curvature at A; the rolling curve is the evolute of (C) that rolls without slipping on the base, which is the normal at A. We derive from this that the glissettes with linear base of a curve are the roulettes with linear base of the evolute of this curve. In this case, we get the following formulas: |
 |
| If the Cartesian parametrization of the sliding curve
in the moving plane is the glissette of the centre of the frame is parametrized by the sliding curve at the instant t is then parametrized by If the polar equation of the sliding curve is then the polar parametrization of the glissette of the pole is Conversely, if the polar equation of the glissette is then the polar parametrization of the sliding curve is |
Examples (see also the roulettes
with linear base, according to the theorem above).
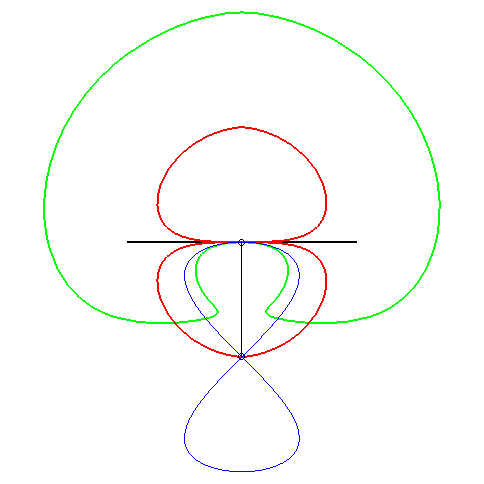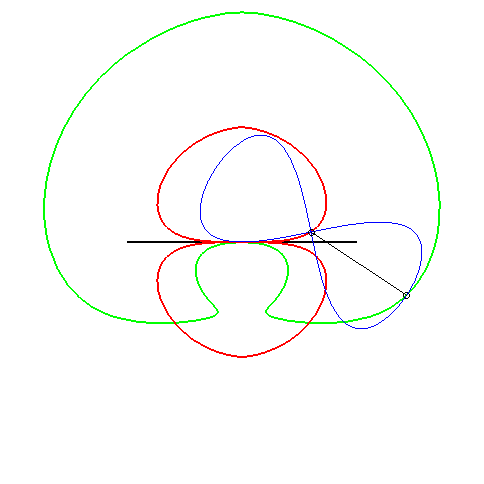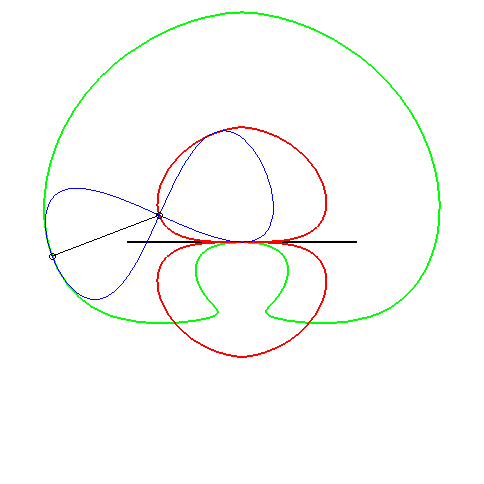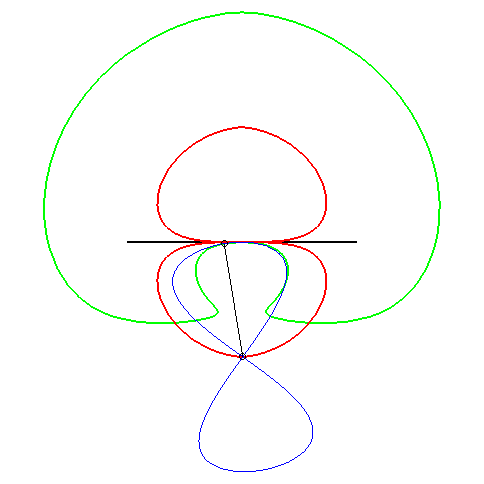
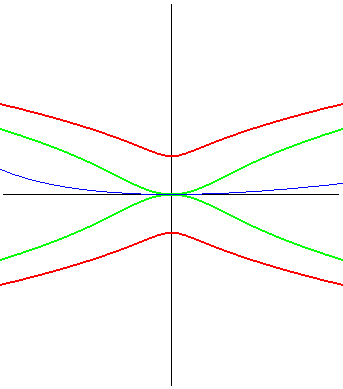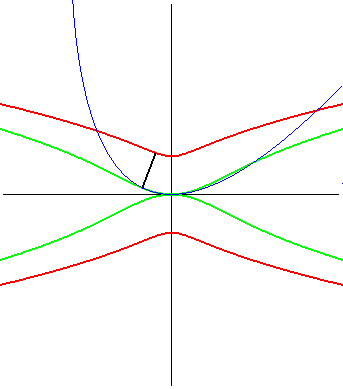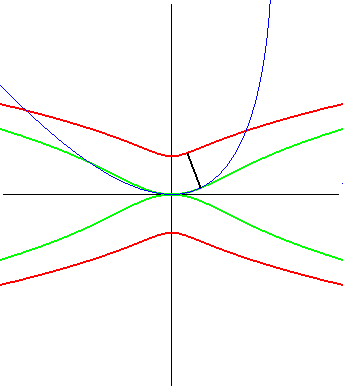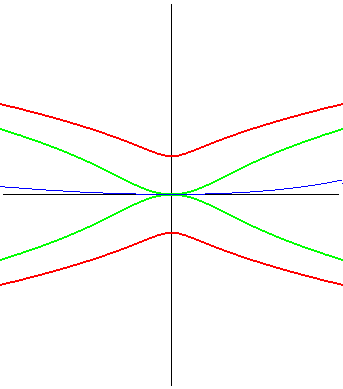
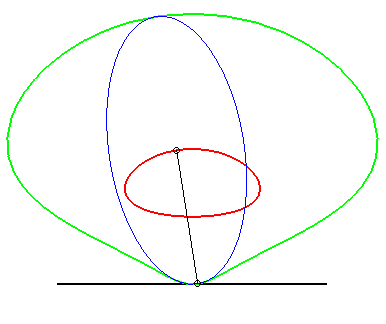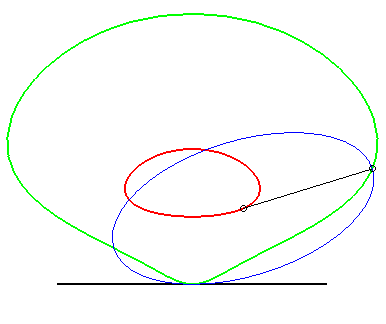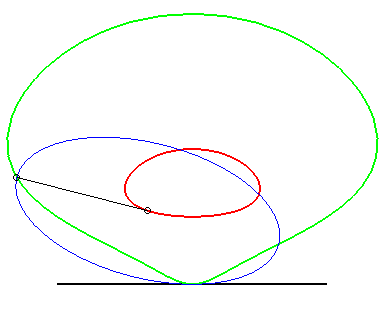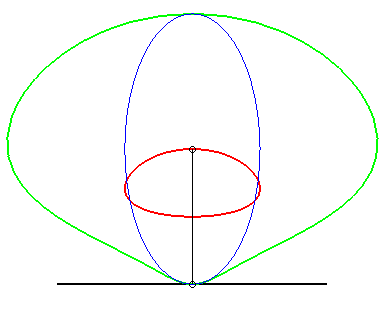
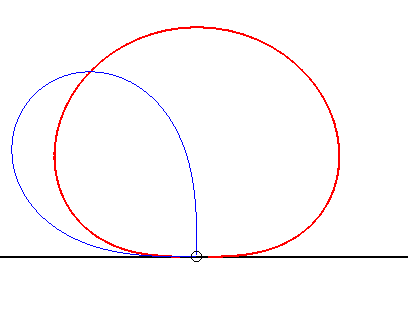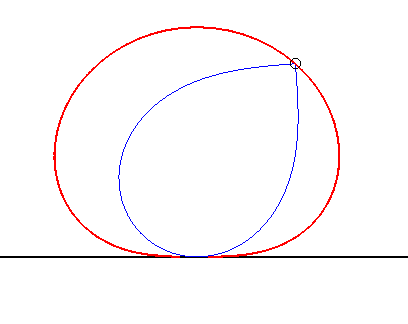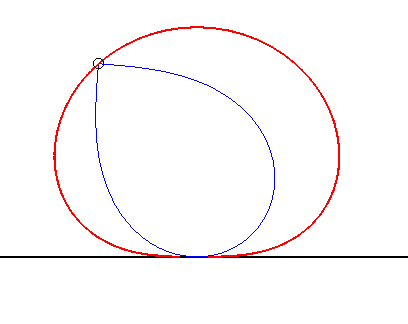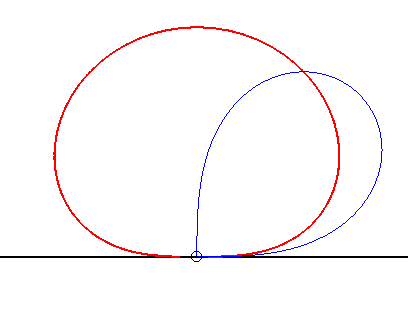
| (1) The glissette of the focus of a parabola is a Kampyle
of Eudoxus; (2) that of the vertex (in green opposite) is the curve
parametrized by
whose equation is: |
 |
| (3) The glissette of the centre of an ellipse is a quartic
of Bernoulli parametrized by (4) The glissette of the centre of a rectangular hyperbola is the Clairaut's curve r² sin q = a². |
 |
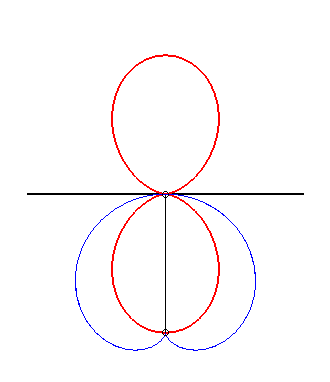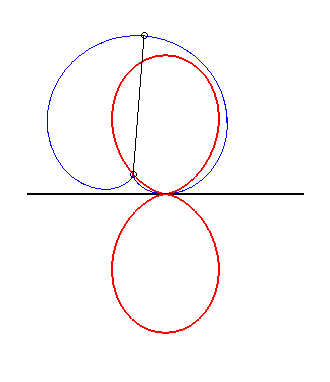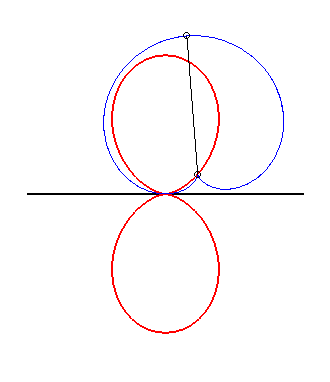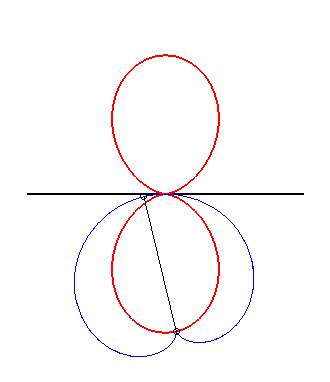
(5) The glissette of the tip of a cardioid
is a double egg.
 |
(6) The glissette of the centre of a lemniscate
of Bernoulli is curve of the dipole.
The previous cases (1),(4),(5),(6) are examples of the fact that the glissettes of sinusoidal spirals |
(7) The glissette of the pole of an involute
of a circle is a straight line (this is normal since the roulette
of the centre of a circle (evolute of the involute) rolling on a line is
a line!)
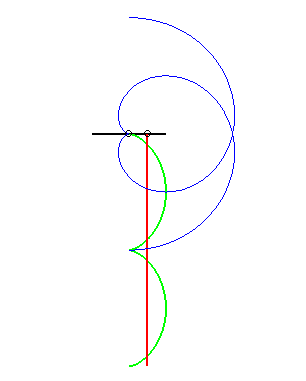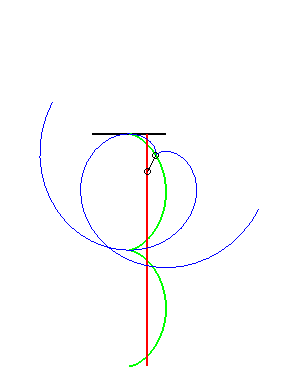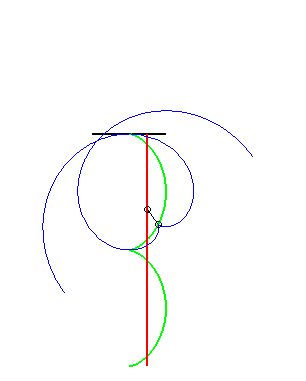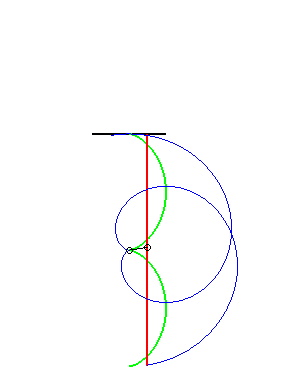 |
(8) The same is true for the glissette of the pole of
a logarithmic spiral (it
is a consequence of the fact that the angle between the tangent and the
radius vector is constant)
The other glissettes are trochoids. 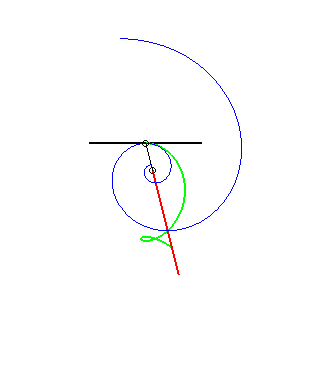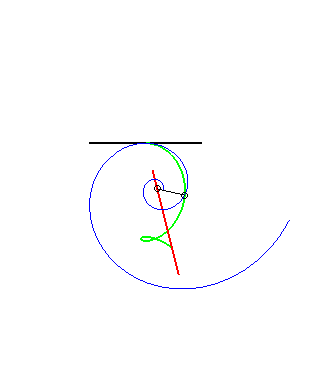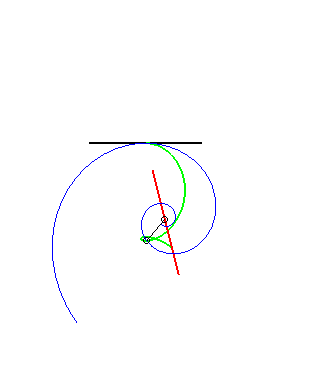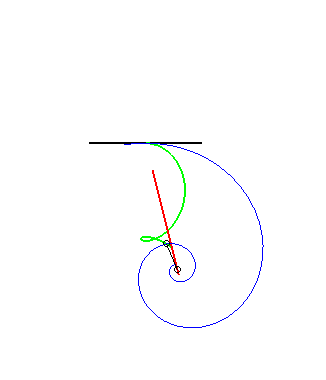 |
(9) The glissette of the pole of an Archimedean spiral
is a Kappa.
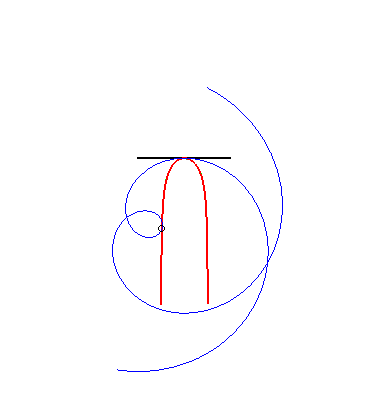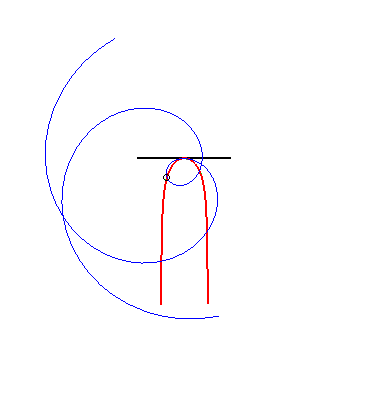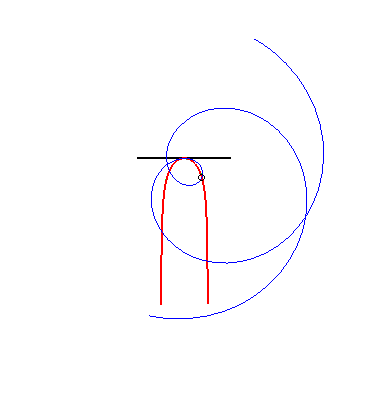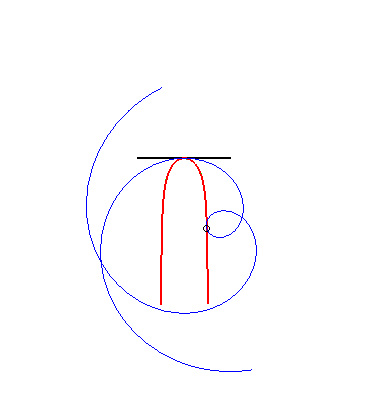 |
(10) The same is true for the glissette of the pole of
a hyperbolic spiral.
|
Last examples: the glissettes of the centre of the fixed circle of a
centred cycloid are ellipses (since it is also the case for their roulettes).
The glissette of the pole of a tractrix
spiral is a circle.
CASE DUAL TO CASE N° 1
| Case where a line slides on a fixed curve (C),
the tangency point A being fixed on the line.
The glissette generated by a point on the sliding line is then none other than an equitangential curve associated to the curve (C). And the glissette generated by a point that is perpendicularly projected on the line on A is none other than a curve parallel to the curve (C). The base of the associated motion of a plane over a fixed plane is the evolute of (C) and the rolling curve is the normal at A. |
SPECIAL CASE N°2
| Case where (C1)
and (C2) are reduced to points A
and B, and (C'1) and (C'2)
coincide like before and are written (C). Opposite, the example
of the glissette of the vertex of a parabola passing by two fixed points.
When B tends linearly to A, the case "tends" to the case n° 1. The dual case is that where the moving plane is carried by two of its points describing a fixed curve (C). See on this page the different examples where (C) is a conic . |
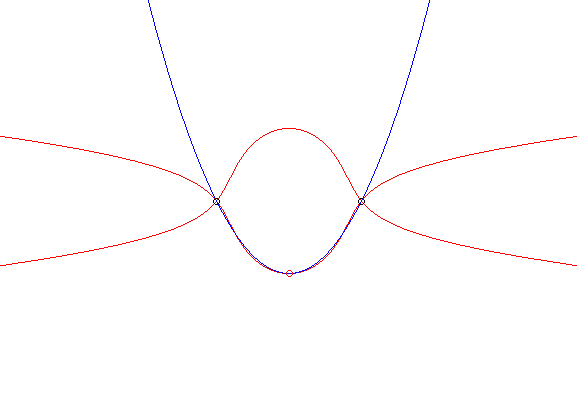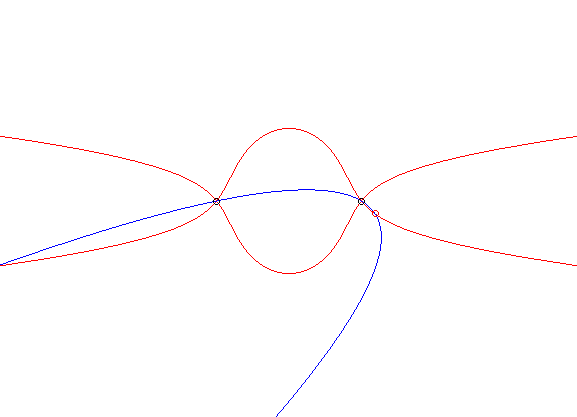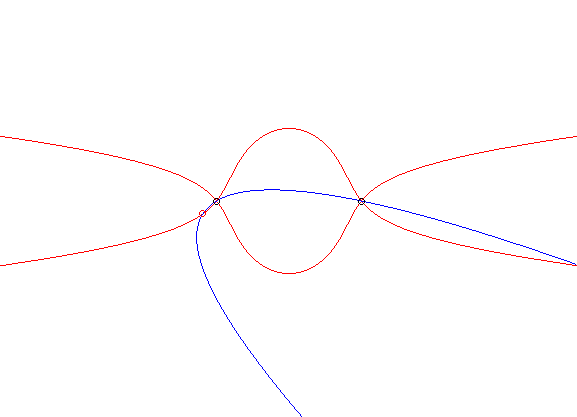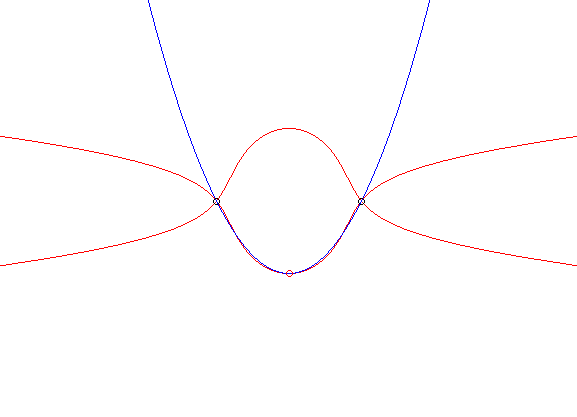 |
SPECIAL CASE N°3
Other examples where the curves (C'1)
and (C'2) are still one and the
same curve (C):
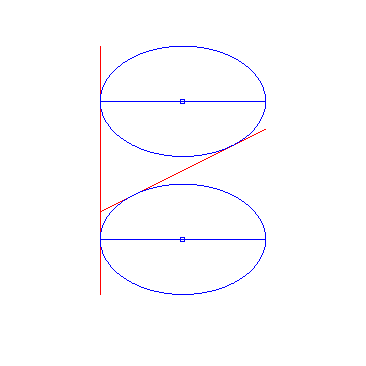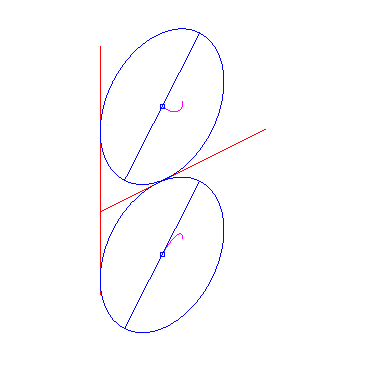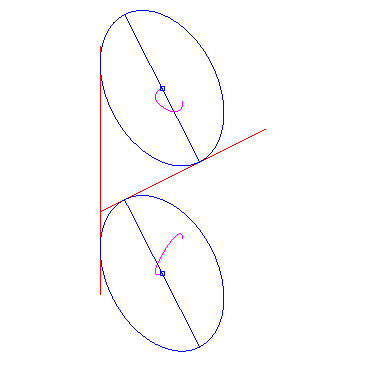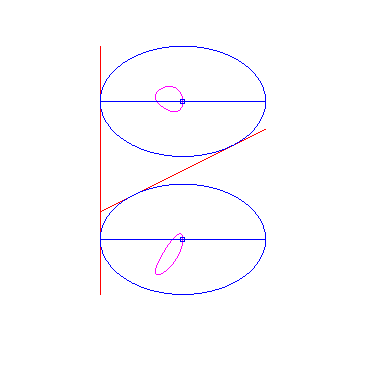
| 1) The two curves (C1) and (C2) are perpendicular lines: | |
| If an ellipse is constrained to remain tangent to two
fixed perpendicular lines, the glissette of the centre of the ellipse is
an arc of a circle (inverse property of the fact that the orthoptic
curve of the ellipse is a circle).
Opposite we added the glissettes of the vertices of the ellipse. The general glissette is parametrized by: For the complete study, see this PhD thesis p. 30. Cf also this animation, showing a very simple articulated system yielding the movement of the ellipse. |
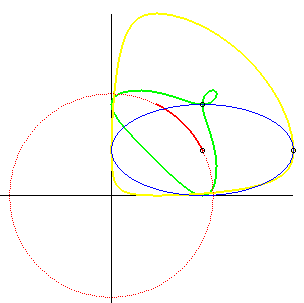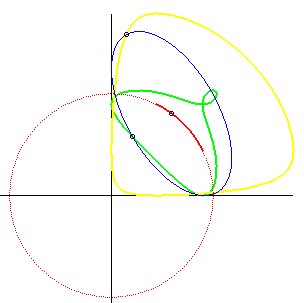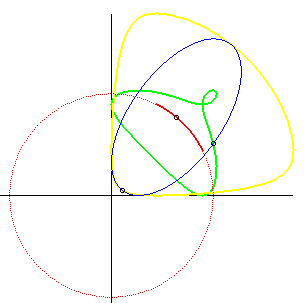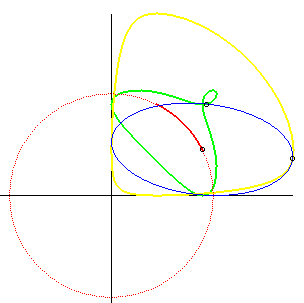 |
| The same is true for the parabola: the glissette of the
focus of the parabola is then a crosscurve;
that of the vertex (in green opposite) is the curve parametrized by: For the base and the rolling curve, see Besant p. 50. |
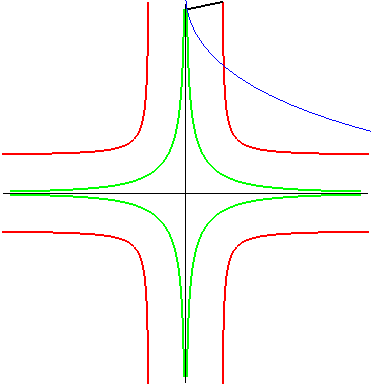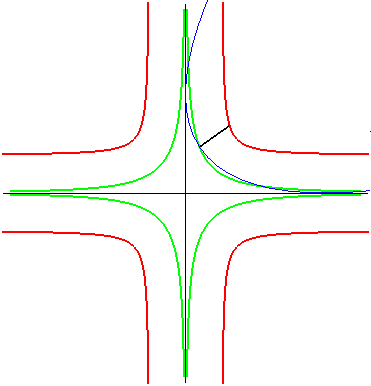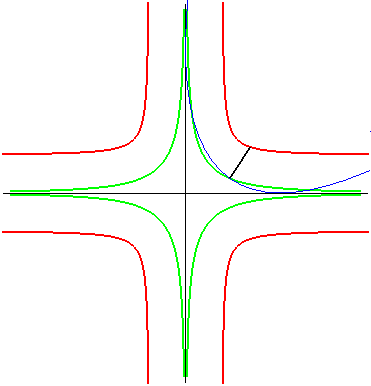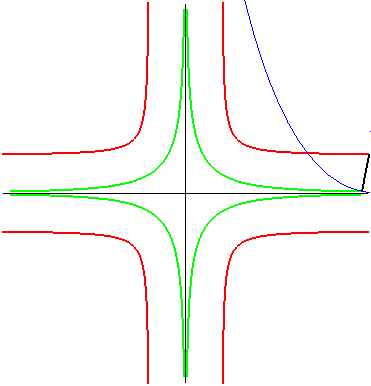 |
| In the dual case, the glissette of the intersection point between 2 perpendicular lines tangent to a curve is none other than the orthoptic curve. |
| 2) The curve (C1)
is a line and (C2) a point not located
on this line.
Example of the glissette of the vertex of a parabola: |
 |
SPECIAL CASE N°4
The curves (C'1)
and (C'2) are reduced to points
like in the case n°2), but (C1)
and (C2) are different: the moving
plane can be visualised well by the movement of a plank with two removable
casters on two rails.
Examples:
| Case where the curves (C1)
and (C2) are perpendicular lines:
the glissettes are ellipses; we
find here the construction of the ellipse by the method called "of the
strip of paper".
Furthermore, the base of the movement of a plane over a fixed plane is a circle, and the rolling curve is a circle with half radius; the points on this rolling curve describe segments of lines: we find here the La Hire device. |
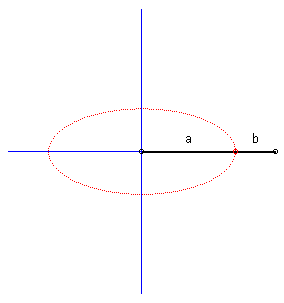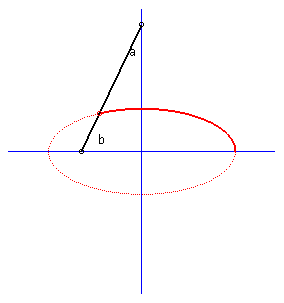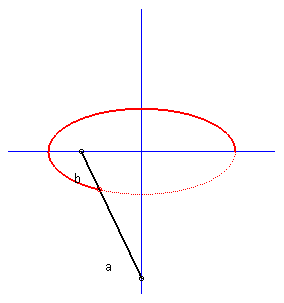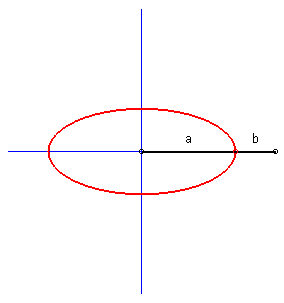 |
|
| If two points on the moving plane slide on two circles, then the glissettes are the curve of the three-bar. |
 |
When one of the curve is a line and the other one a circle, we get the curves of the slider-crank mechanism and, more generally, when one of them is a line and the other one is a conic, we get the polyzomal curves. |
DUAL CASE OF THE CASE N°4
(C1) and (C2)
are reduced to fixed points M1 and
M2
, and the two curves (C'1) and (C'2)
are required to pass through M1
and M2.
|
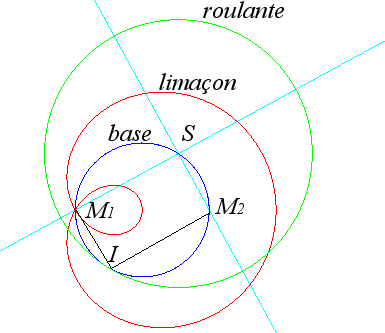
Case where (C'1) and (C'2) are two perpendicular lines. Their point of intersection S describes the circle of diameter [M1M2]. The points on the line (M1S) remain at constant distance from S, therefore describe a "conchoid" of the circle described by S, of pole M1, which belongs to this circle. It is a Pascal's snail. We let the reader understand from the figure the construction of the base and the rolling curve which are, as expected by duality, a circle and a circle of double radius, the first circle being precisely that described by S. This allows to see that all the glissettes are Pascal's snails. |
 |
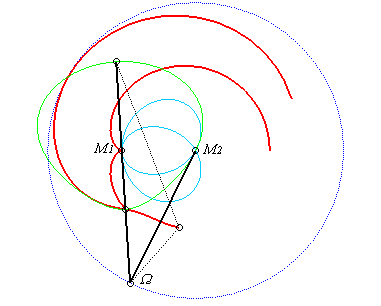
| Cas où (C'1)
est (C'2) sont respectivement une
droite et un cercle centré sur cette droite.
Il faut placer une barre double fixée en M2 et articulée en Les glissettes de points qui sont sur la deuxième branche tracent des « conchoïdes » du cercle lieu des points Case where (C'1)
and (C'2) are respectively
a line and a circle centered on this line.
|
 |
SPECIAL CASE N°5
| (C'1) and (C2) are reduced to points; i.e., a curve (Cm) of the moving plane passes by a fixed point Af , and a point Am of the moving plane describes a fixed curve (Cf). Note that the dual case is then of the same type. | |
| If the moving curve is a line and the moving point is
located on this line, the glissettes of the points on the moving line are
none other than the conchoids
of the fixed curve with respect to the fixed point. The others are isoconchoids
of it.
Opposite, the case where the fixed curve is also a line. We recognize indeed, in red, a conchoid of Nicomedes; in green, two isoconchoids. The associated movement of a plane over a fixed plane, called conchoidal movement, is studied on this page. |
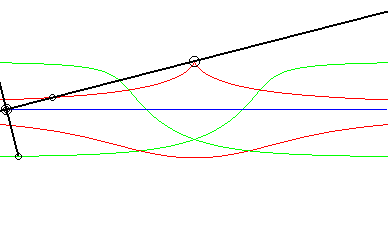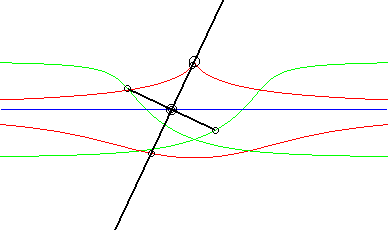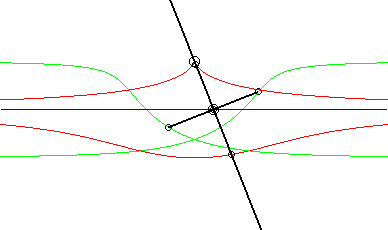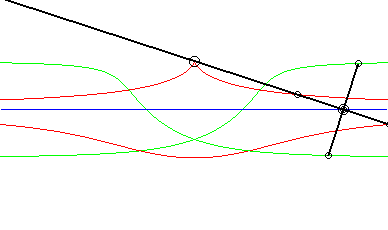 |
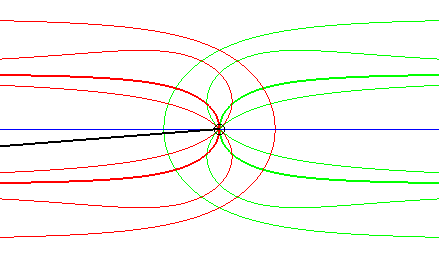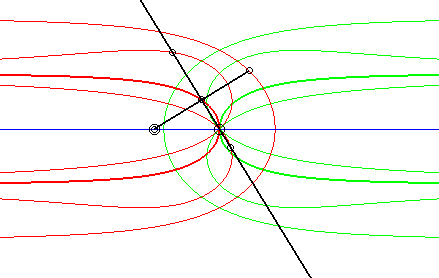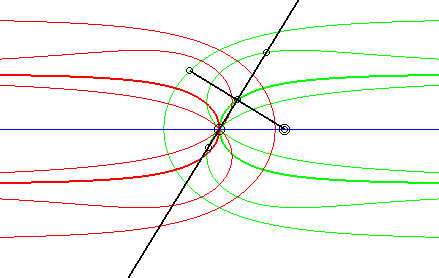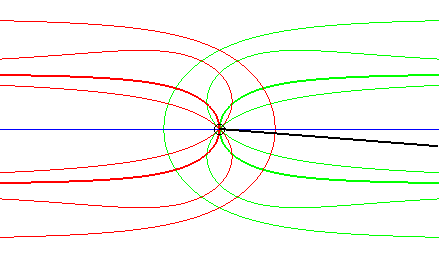
| In the dual case, the fixed curve is a line and the fixed
point is on this line; the moving curve passes by this point and the moving
point describes the line.
Opposite, the case where the fixed curve is also a line. The glissette of the projection of the moving point on the moving line is a Kappa (in bold), hence the name of the associated movement of a plane over a fixed plane: the Kappa movement (see this page). The other glissettes are conchoids, or isoconchoids, of
the Kappa with respect to its centre.
|
 |
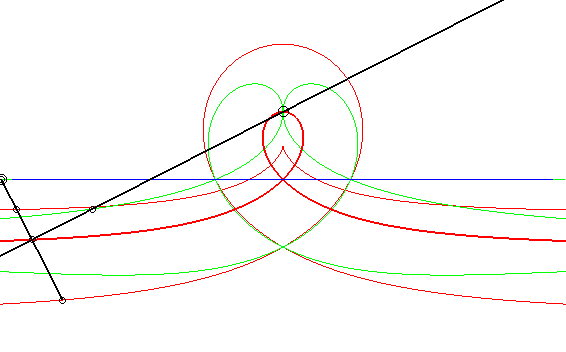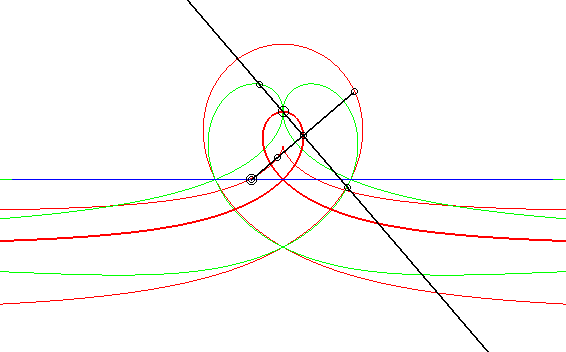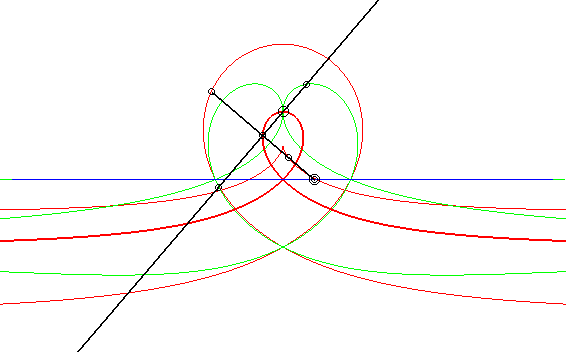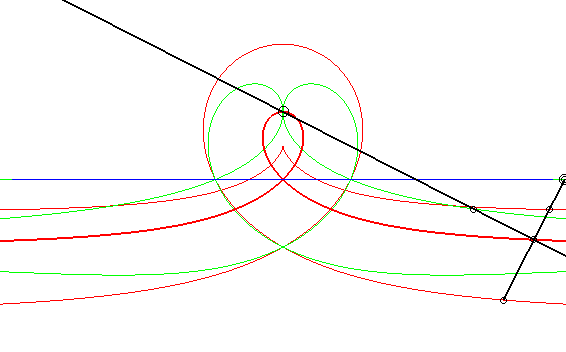
| Case where the fixed and moving curves are lines, the
fixed and moving points being at the same distance to their associated
line.
The glissettes of the points on the line passing by the moving point and perpendicular to the moving line are the right rational circular cubics. We recognize here the mechanism called "Newton's set square" used to trace cubics. In particular, the glissette of the projection of the moving point on the moving line is a right strophoid (in bold opposite). The other two red curves are the right cissoid and the Maclaurin trisectrix. The glissettes of the points on the moving line are the conchoids of the right strophoid with respect to its vertex, i.e. any strophoid (two examples in green opposite). The other glissettes are isoconchoids of the right strophoid
with respect to its vertex.
|
 |
SPECIAL CASE N°6
| (C'1) is a line
(D), and (C'2) is a point
A
of this line.
In other words, a point A of a connecting rod (D) is forced to move on a curve (C2) while remaining tangent to a curve (C1). |
 |
| Example: (C1)
is a circle of radius a and (D) is a tangent to this circle.
We look at the glissette of a point of the connecting rod located at a distance b from A. Parametrization : Cartesian equation : The basis of the plane-on-plane movement is the parabola with focus the center of the circle and directrix the fixed tangent and the rolling one is the parabola with focus A and directrix parallel to the mobile tangent passing through the center of the circle. |
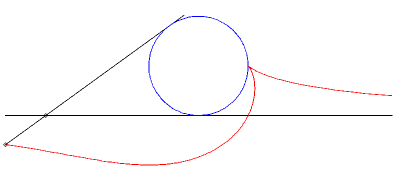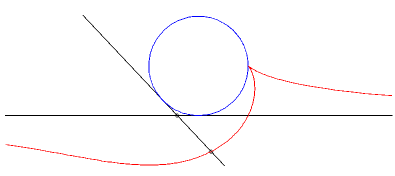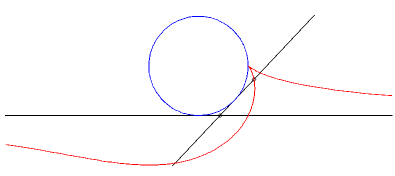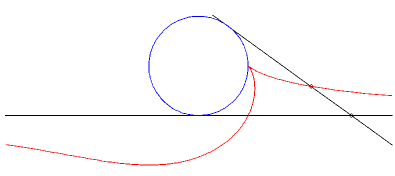
Case a = b : rationnal cuspidal cubique. |
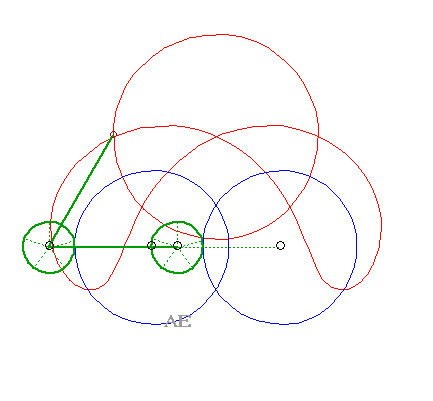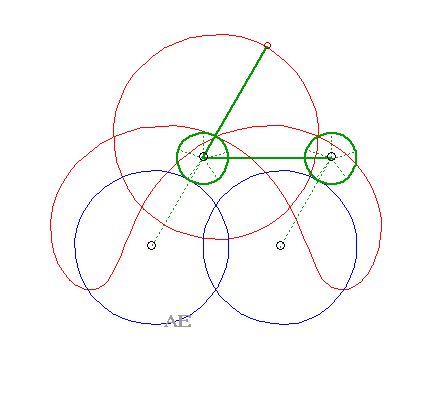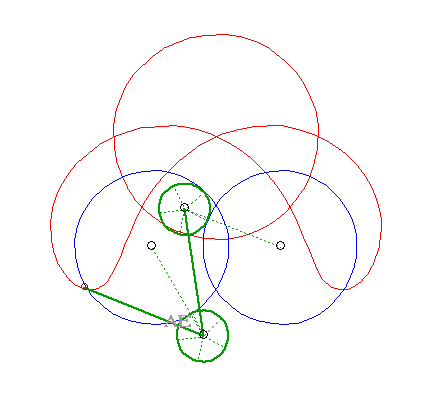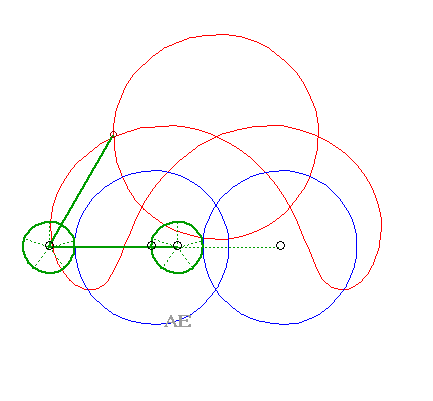
SPECIAL CASE N°6
| The 4 curves (C1)
and (C2), (C'1)
and (C'2) are circles.
The glissettes are none other, again, than the curves of the three-bar. |
 |
This can be generalized by adding a constraint, but allowing
the moving plane to be only similar to the fixed plane, and no longer isometric
to it.
Examples:
| If the focus of a parabola is fixed, and the parabola is constrained to pass by a fixed point, then the glissette of the vertex of this parabola is a cardioid: |  |
| Conversely, if the vertex of a parabola is fixed, and the parabola constrained to pass by a fixed point, then the glissette of the focus of this parabola is a cissoid of Diocles: | 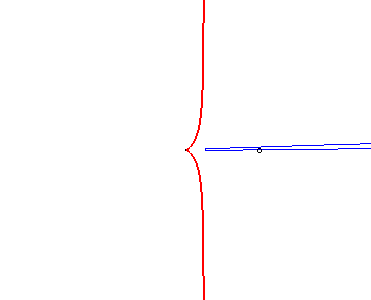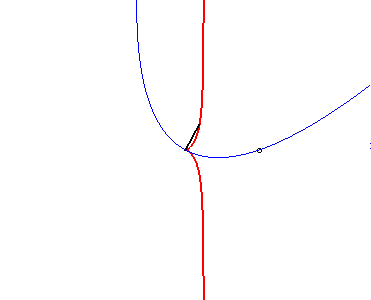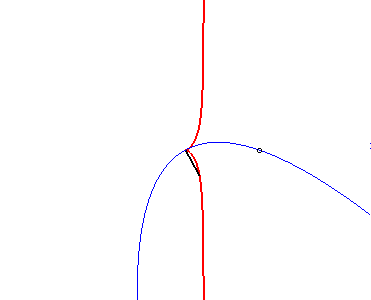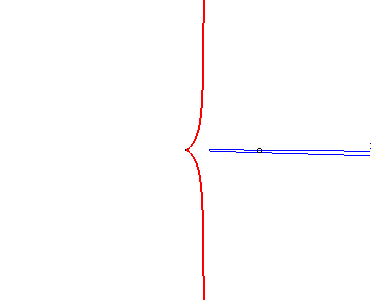 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Alain ESCULIER 2017