Slider-crank mechanism

CURVE OF THE SLIDER-CRANK MECHANISM

Above on the left, only half of each curve is drawn. They should be completed by their symmetrical image about (OA).

Curve studied by Bérard in 1820 and Ruiz-Castizo in 1889.
Other name: Ruiz-Castizo's quartic.

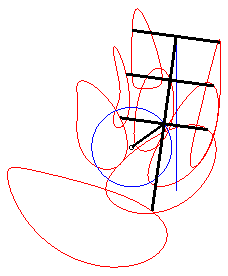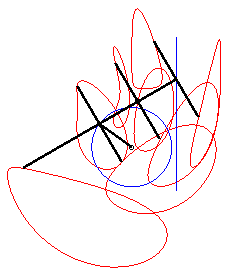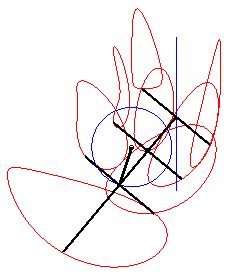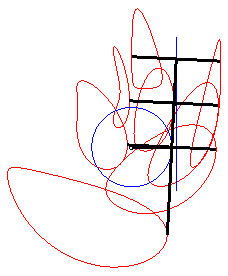
The curve of the slider-crank mechanism is the locus of a fixed point M on the plane linked to the bar [PQ] (called the connecting rod) of an articulated mechanism (OPQ), O being fixed and Q being constrained to move on a line (D) (the drawer, or piston). In other words, the curve of the slider-crank mechanism is the locus of a point linked to a segment line of constant length joining a circle (C) and a line (D).

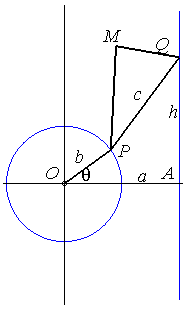Let A(0, a) be the projection of O on (D), OP = b, PQ = c.
Using lower case letters for the affix of a point, we have:

With , and we get:
Cartesian parametrization:
, where with following the position of Q with respect to (OP).
Specifically, the motion of Q is not sinusoidal.
Bicircular quartic (?).
Cartesian equation when M is on the line (PQ) (i.e. l = 0):
.

The curve is not empty if and only if a £ b + c, and in that case it is connected iif b £ a + c (?).

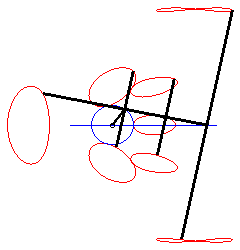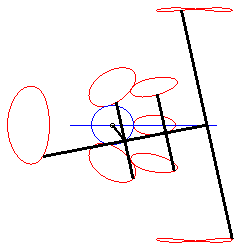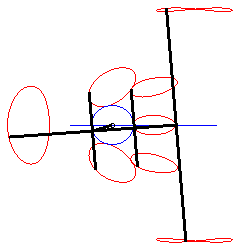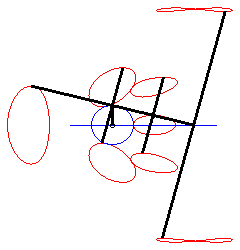
When M is on the connecting rod, the equation above shows that the curve is then a polyzomal curve, medial between two ellipses: , and .

In particular:

- when a = 0 ((D) passes by O) and k = -1, these two ellipses are concentric circles: the associated curves are the quartics of Bernoulli. See also on this page the base and rolling curve of the planar movement on the associated plane.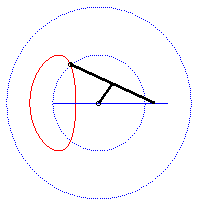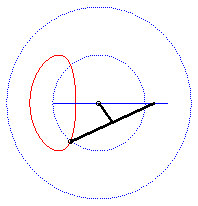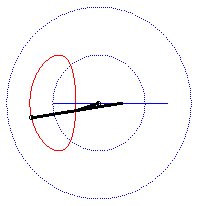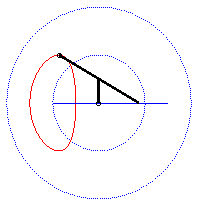

- when c = a + b and k = -1, these two ellipses are tangent circles: the associated curves are the double heart curves.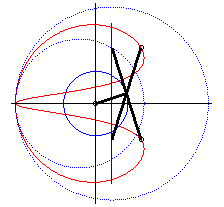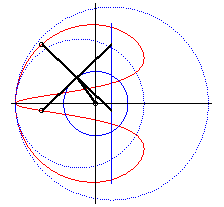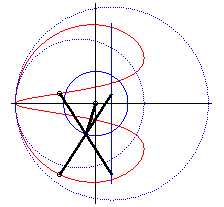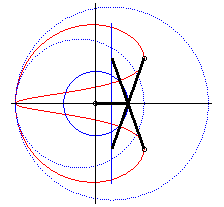

- when a = 0 and b = c, the curve of the slider-crank mechanism is composed of a circle and an ellipse (in fact, we find the construction of an ellipse with a strip of paper).

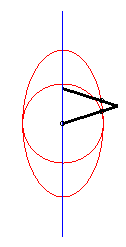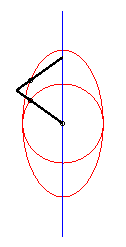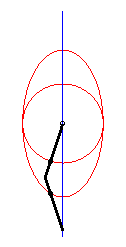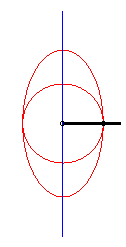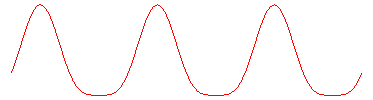
This device allows for a linear, almost sinusoidal motion; on the right is the representation of the movement of Q for a = 0, b = 1, c = 3.
See also an application to Mercedes's windscreen wiper.

If the circle (C) is replaced by any conic, we get all the polyzomal curves.

If the line (D) is replaced by a circle, we get a curve of the three-bar mechanism.

If the connecting rod is no longer constrained to have its end sliding on a line but is only constrained to slide while passing through a fixed point, we get the conchoids of circles.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra

- when a = 0 ((D) passes by O) and k = -1, these two ellipses are concentric circles: the associated curves are the quartics of Bernoulli. See also on this page the base and rolling curve of the planar movement on the associated plane.
- when c = a + b and k = -1, these two ellipses are tangent circles: the associated curves are the double heart curves.
- when a = 0 and b = c, the curve of the slider-crank mechanism is composed of a circle and an ellipse (in fact, we find the construction of an ellipse with a strip of paper).