Polyzomal curve

POLYZOMAL CURVE

Curve studied and named by Cayley in 1868; the mechanical generation was studied by Ruiz Castizo in 1889.
From the Greek zoma "belt".

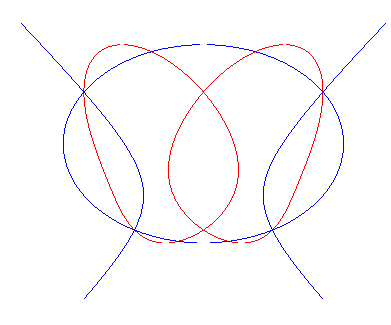
Cartesian equation:

, i.e.

where P and Q are polynomials of degree

2;
Quartic (of genus 1) with a symmetry axis.

The polyzomal curves are the median curves of two conics with a common axis, along a perpendicular to this axis; indeed, writing the equation above as , it can be noted that it represents the median curve of the two conics with axis Ox: and .

The polyzomal curves include all the quartics with a symmetry axis having one or two double points on the axis (possibly imaginary)(??).

Ruiz-Castizo proved that they could be generated from a conic (C) and a line (D) by making a segment line [PQ] with constant length slide, while P is constrained to stay on the conic (C) and Q on the line (D), and considering the locus of a point M on the line (PQ) (see [Gomes Texeira T2] page 308); when the conic (C) is a circle, we get the special case of the slider-crank mechanism.

When the two conics are tangent circles, we get the doubles hearts and when the conics and are a parabola and its osculating circle at the vertex, we get the regular bifolium.

When the two conics are concentric circles, we get the Bernoulli quartics.

When the two conics are parabolas in opposite directions, we get the besaces (including the lemniscate of Gerono when the parabolas are isometric).

In fact, the definition of the polyzomal curves by Cayley is far more general; they are the algebraic curves the equation of which can be written where the U_i are polynomials with maximum degree m; the curve is then of degree ; each curve U_i(x,y) = 0 is a zomal, or belt, of the curve. Cayley showed that the trizomals with m = 2 are exactly the quartics; the curves above are a special case.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra