Drawbridge curve

DRAWBRIDGE CURVE

Curve defined by Bernard Forest de Bélidor during his study of the drawbridge mechanism that since bears his name.
He had himself named this mechanism: drawbridge with a sinusoid, even though the curve is not a sinusoid.

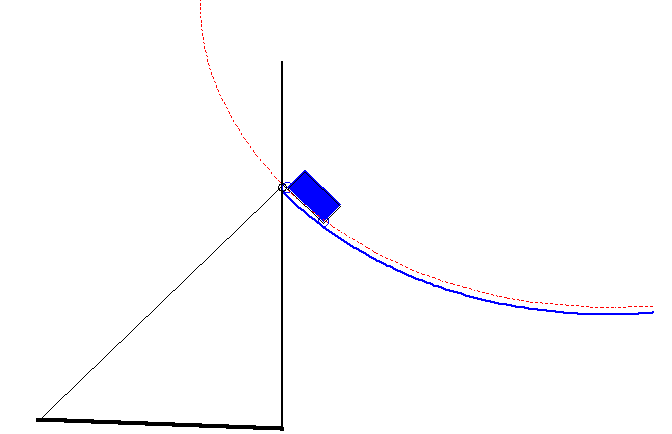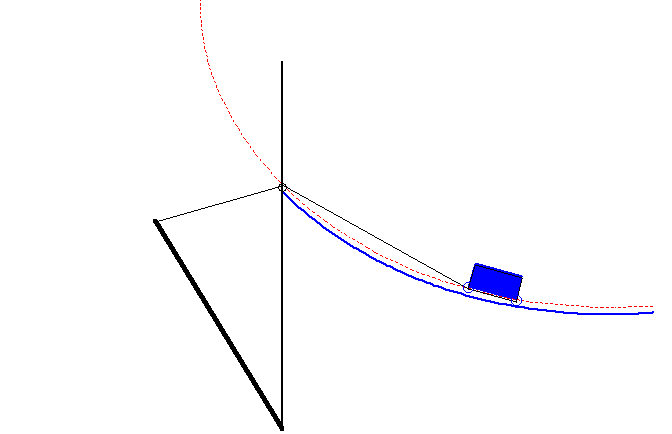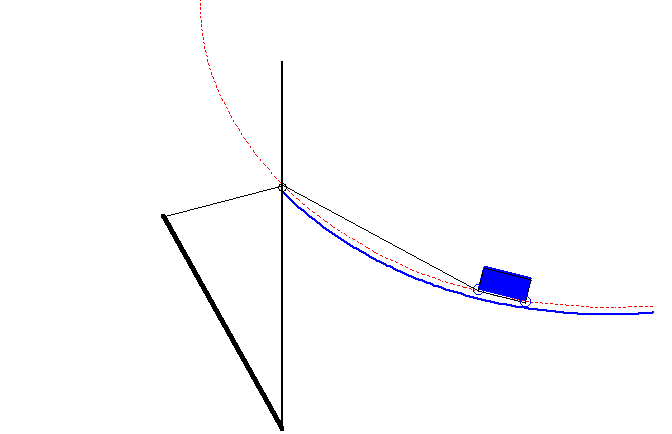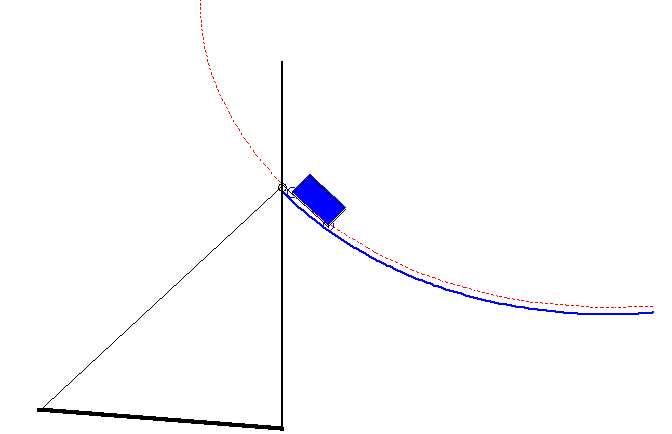
The drawbridge curve is the curve described by the end of the counterweight of a drawbridge (figure above) so that the system bridge + counterweight is always in equilibrium.

It can be proved that this curve is none other than a portion of Cartesian oval.

Here is a proof of this fact:

With the notations of the opposite figure, we write that the total potential energy is constant: ; by eliminating a between this relation and the Al-Kashi relation: , we get , which is indeed the equation of a Cartesian oval, that reduces to the limaçon of Pascal if . The point C is a focus of the oval.
If we consider the case where the counterweight is at C when the bridge is down, then the constant E equals 0 and ; the drawbridge curve is still the limaçon of Pascal , which is a cardioid if .
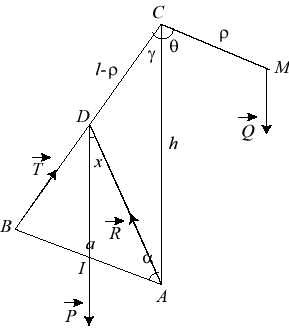
In the general case, if and when the drawbridge is down, then and the oval is a limaçon if or .
a = length of the drawbridge = AB
l = length of the hoist = BC+CM
P = weight of the drawbridge
Q = weight of the counterweight

Calculation of the tension of the hoist: since the bridge is in equilibrium, the sum of the moments of the forces applied to it is zero: ; we get .

A drawbridge with the Bélidor system can be found in Fort l'Ecluse (not far from Geneva).

Other curves defined mechanically: the curve of the water bucket, the curve of the tightrope walker.

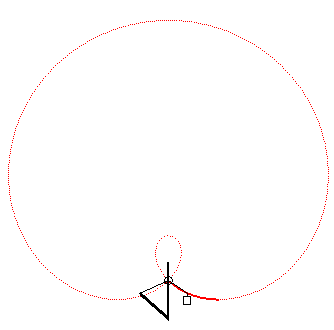
Case where the curve of the drawbridge is a portion of a limaçon of Pascal
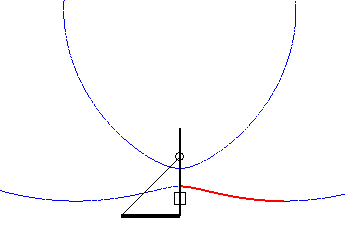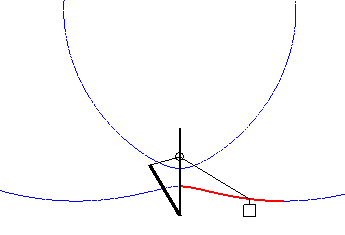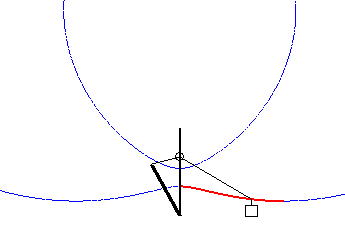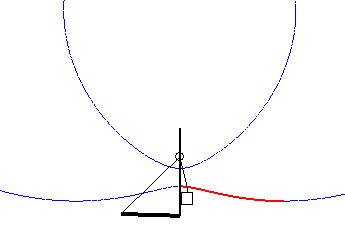
Case where the drawbridge curve is a portion of a Cartesian oval.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra