SUSPENSION BRIDGE CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
SUSPENSION BRIDGE CURVE
| Curve studied by François Lavallou in 2008 (Tangente Sup n° 46). |
If 
and  are
the respective linear mass densities of the cable and the bridge, 
the tension of the cable at the bottommost point,  ,  ,  ,  ,
then:
Cartesian parametrization:  .
Curvilinear abscissa:  . |
The suspension bridge curve is the shape assumed by an
inextensible homogeneous infinitely thin flexible massive wire hanging
from two points, placed in a uniform gravitational field, and to which
is hanged, by infinitely many wires, a massive horizontal line (the bridge).
Note that in reality, there is only a finite number of
suspension wires, so the bridge also rests upon the furthest columns.
With the notations of the opposite figure and that of
the boxed text above (
= tension of the wire at M, 
= linear mass density of the suspension wire,
that of the suspended wire), we write that the sum of the forces at M
is zero:
This simplifies to |
 |
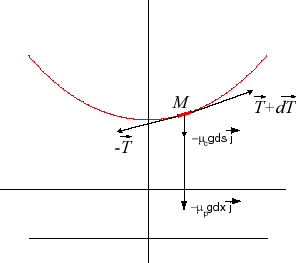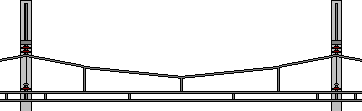
If we trace a family of suspension bridge curves with
same length for values of k ranging from 0 (mass of the bridge <<
mass of the cable: catenary)
to infinity (mass of the bridge >> mass of the cable: parabola),
we get the figure opposite and below, which show that the various curves
are not very different; the sagitta of the parabola being slightly larger
than that of the catenary.
 |
 |
For a real suspension bridge, we can consider that the mass of the cable is negligible in comparison to that of the bridge, so the cable assumes the shape of a parabola.
In case of railway catenaries, the upper cable and the
contact cable have masses of the same order of magnitude and so we could
consider that the previous reasoning holds but, in reality, there are far
too few suspension cables and the upper cable is rather shaped like a broken
line...
 |
 |
 |
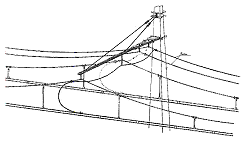The integral formulas above can be calculated for different
values of k:
|
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018
,
which, by integration, gives 
.
which, by differentiation, gives the differential equation 
;
and this yields the parametrization above by taking: 
.
