Rectangular hyperbola

RECTANGULAR HYPERBOLA

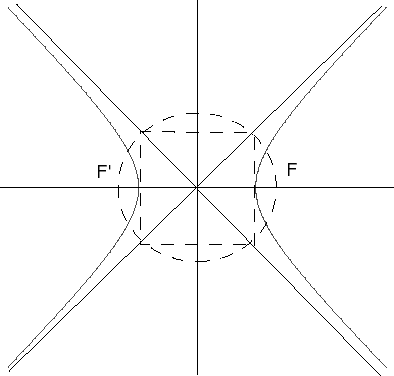Reduced Cartesian equation:

. In the frame turned by an eight of a turn:

.
a = semi-major axis;
foci: F(

, 0) and F'(-

, 0) .
directrices: lines with equation x =

and x = -

Cartesian parametrization:

(with

; form used in the following).
or

(with

).
Polar equation:

(it is therefore a special case of sinusoidal spiral).
General polar equation of a rectangular hyperbola passing by O:

(complex parametrization:

)
Curvilinear abscissa:

.
Radius of curvature:

.
Bifocal equation:

.
Tripolar equation : MF.MF' = OM², O midpoint of [FF'].
Polar equation (pole F, axis Fx):

The rectangular hyperbola is the hyperbola for which the axes (or asymptotes) are perpendicular, or with eccentricity . It is to general hyperbolas what the circle is to ellipses.

Here are various geometrical definitions:

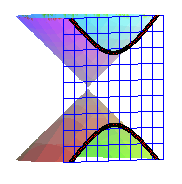
1) Conic definition:
The hyperbola is the section of a rectangular cone of revolution (angle at the vertex equal to 90°) by a plane strictly parallel to the axis of the cone.

2) Bifocal definition:
The rectangular hyperbola is the locus of a point M such that the difference of the distances to two fixed points F and F' is equal to times the distance between these two points (see the bifocal equation).

3) Definition by focus and directrix:
The rectangular hyperbola is the locus of the point M such that where H is the projection of M on the directrix (D).

4) Cissoidal definition:
Given two perpendicular lines and a point A outside of these lines, the locus of the points M such that , where P and Q are the two intersection points between the two lines and a variable line passing by A, is the hyperbola passing by A and whose asymptotes are the two initial lines. (we derive easily from this that the hyperbola is the cissoid of the two perpendicular lines).

5) a) Angular definition (special case of stelloid):

Given two different points A and B, the locus of the points M such that the bisectors of the lines (MA) and (MB) have constant directions is the rectangular hyperbola passing by A and B whose asymptotes pass by the middle of [AB] and are parallel to these constant directions.
Mechanical interpretation*: a rope is attached at an end to a fixed point A, passes by a pulley B and is maintained by hand at the other end. A bucket hangs from the rope thanks to a pulley between A and B.
The bucket describes a portion of rectangular hyperbola.
* See Roguet p 161 (1842)

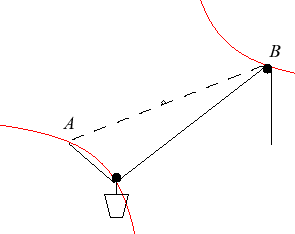Curve of the bucket: compare to the curve of the tightrope walker.

b) Angular definition equivalent to the previous one .

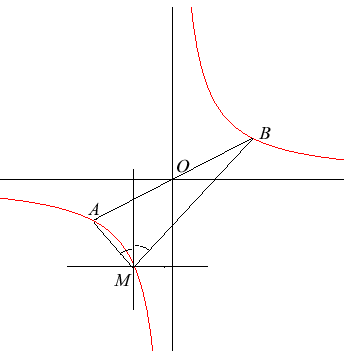
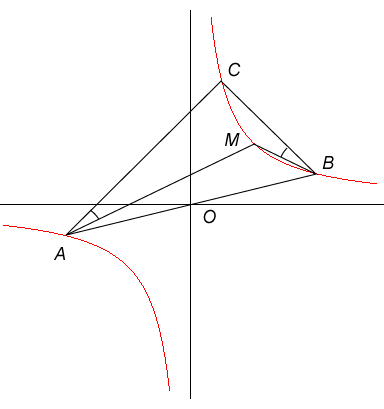
Given three distinct points A, B, C the locus of points M verifying (AC, AM) = (BM, BC) (oriented angles of lines) is the unique equilateral hyperbola of diameter [AB] (i.e. centered at middle of (A, B)), possibly degenerate, passing through C. The asymptotes are parallel to the bisectors of (AC) and (BC).

(1) also written: (AB, AM) – (BM, AB) = (AB, AC) – (BC, AB), we can give a third angular definition:
given two distinct points A,B, and a real the locus of the points M verifying measure(AB, AM) – measure(BM, AB) = mod is a rectangular hyperbola of diameter [AB].
For example, measure(AB, AM) – measure(BM, AB) = mod gives the rectangular hyperbola of vertices A and B.

The previous definition allows the construction opposite [J. Lemaire, hyperbole équilatère, p. 1] of the rectangular hyperbola of vertices A and B from the circle of diameter [AB] .
The point P traveling through the circle, the angles verify and we have, in the case of the figure where , for the triangle (AMB) : . The point M here describes a branch of the hyperbola, the other branch being obtained for .
Analytically, with A(a, 0) and B(-a, 0), the transformation is defined by (harmonic homology of center B and axis x = a), therefore the circle is indeed transformed into the hyperbola .

6) Strophoidal definition:

The rectangular hyperbola is the strophoid of a line (D) with respect to a point O outside (D) and a point A located at infinity on a perpendicular line.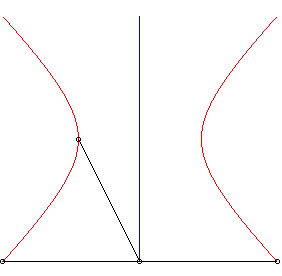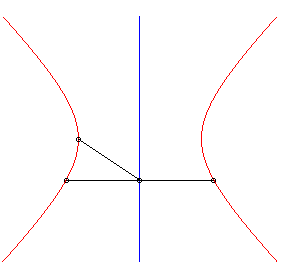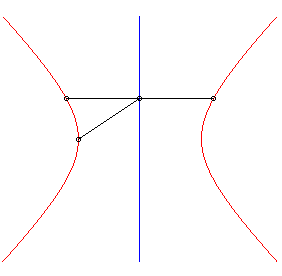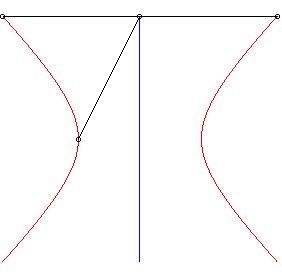

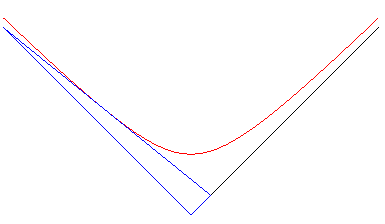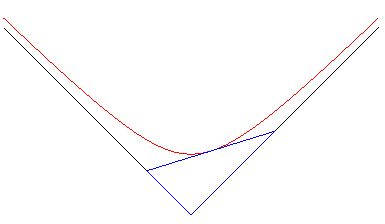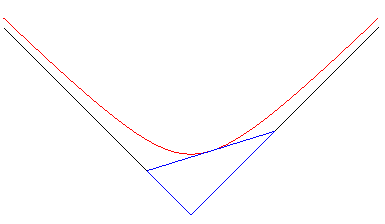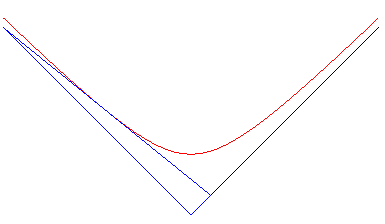
7) Definition as the envelope of a triangle with constant area.

The rectangular hyperbola is the envelope of the segment line [AB] the ends of which move on the orthogonal axes Ox and Oy in such a way that the oriented triangle OAB has a constant area.
The contact point in the middle of [AB].
Therefore, if we consider a cubical container, full of a coloured liquid, an edge of which remains horizontal, the trace left by the liquid on the edges when the container is pivoted is delimited by a hyperbola.
This property still holds in the case where the lines are not orthogonal; the envelope is then any hyperbola.
The 3D generalisation of this problem gives the surface xyz = constant.

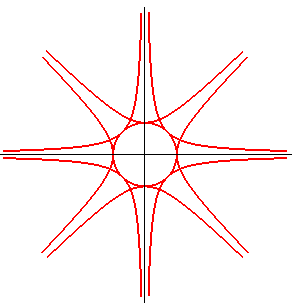
Figure showing the four rectangular hyperbolas and , along with the circle .