CISSOID OF TWO CURVES

From the Greek Kissos: ivy.

Polar equation of the cissoid of pole O of the curves and : .

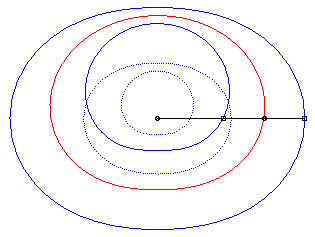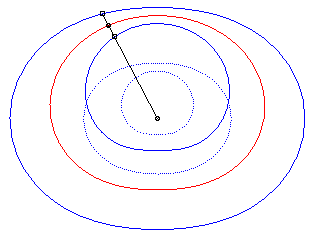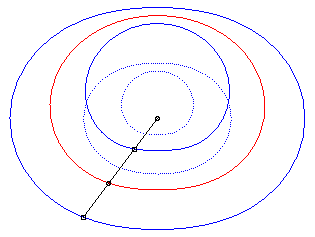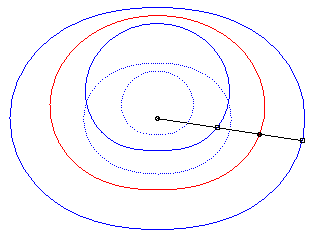
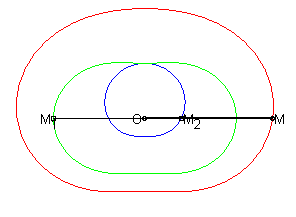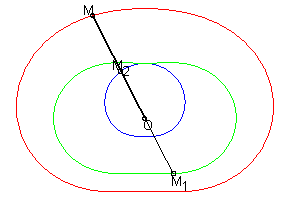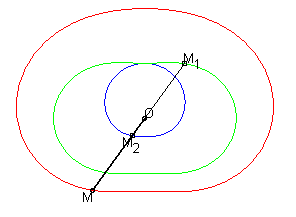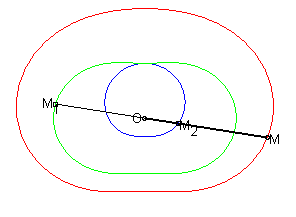
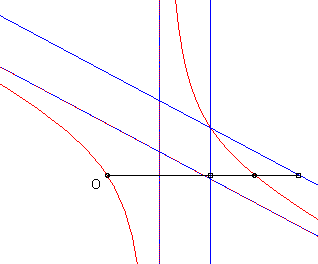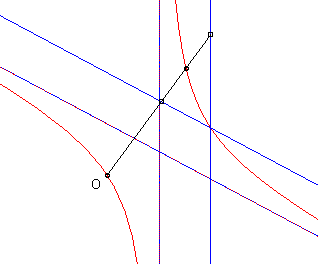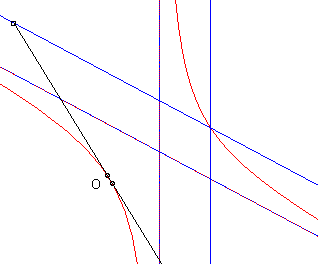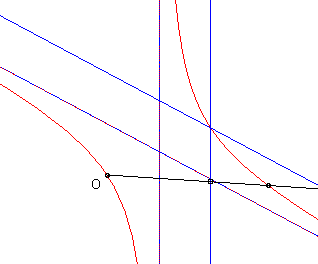
The cissoid of two curves and with respect to a point O is the locus of points M such that where M₁ is a point on and M₂ is a point on , with M₁, M₂ and O aligned.

Therefore, the cissoid is the medial curve of pole O of the curves and , the images of and by the homothety of centre O and ration 1/2.

In dotted lines, the curves (G₁) and (G₂), in blue, the curves (G'₁) and (G'₂) the medial of which is the cissoid. Remark: the cissoid of the cissoid and the symmetrical image of one of the initial curves with respect to O is the other initial curve.

Sometimes, the cissoid is defined as the locus of points M such that ; this amounts, of course, to changing into its symmetrical image about O in the definition we adopted.

Examples:
- when

and

are two parallel straight lines, the cissoid is a third parallel line.
- when

and

are two secant straight lines, the cissoids are the hyperbolas passing through O, with asymptotes

and

In mauve, the two lines, and in blue their homothetic image, of which the hyperbola is the medial curve. - when (G₂) is a circle a and O is its centre, we get the conchoids of the curve

.
- when

is a conic,

is a line, and O is on the conic, we get the cissoids of Zahradnik.
- when

and

are circles and O is on one of them, we get the rational bicircular quartics.
- when

and

are circles and O is in the middle of the two centres, we get the Booth curves, of which the lemniscate of Bernoulli is an example.

- The parabolic folium is the cissoid of a line and a semicubical parabola.

- the beetle curves are the cissoids of a circle and a four-leaved rose.

Remark: when the two curves and coincide, the cissoid is composed of the image of it by the homothety of centre O and ratio 2, but also, possibly, of another part (because the points M₁ and M₂ can be different).

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra