From the Greek huperbolê "over-thrown or excessive", from huper "above, beyond" and ballein "throw". Name given by Apollonius of Perga. See on this page by Alain Esculier the programs to draw the animations.

 

Reduced Cartesian equation: . a = semi-major axis (or transverse), b = semi-minor axis (or non-transverse). = linear eccentricity. = eccentricity, p =  = semi-latus rectum. F(c, 0) et F'(– c, 0): foci of the hyperbola. (D), (D'), lines with equation x = a2/c et x = – a2/c : directrices of the hyperbola. K: foot of the directrix on the axe Ox. d = FK  = b2/c . The hyperbola is said to be rectangular when a = b, i.e.  , that is to say when the asymptotes are perpendicular. The hyperbola with eccentricity equal to 2 is a trisectrix.

Cartesian equation in the frame associated to the asymptotes: XY = , the frame being orthogonal iff the hyperbola is rectangular. Cartesian parametrization:  (with ; form used in the following). or  (with ). Polar equation: . Curvilinear abscissa: . Radius of curvature: . Bifocal equation: . Polar equation (pole F, axis Fx): . Cartesian and polar equations in a frame with origin at the vertex and abscissa axis the focal axis: , .

The hyperbolas are the conics with eccentricity  > 1.

They have been historically defined as section of a cone of revolution by a plane forming, with the axis of the cone, an angle smaller than that formed by a generatrix and the axis.
 

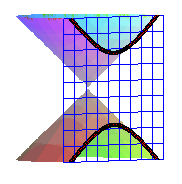
hyperbola = non-connected intersection of a cone and a plane

Application: the boundary of the trace of a light cone on a wall is hyperbolic, if it is unbounded.

But, more generally, any section of a quadric by a plane, with two connected components, is a hyperbola.

The hyperbola has many planar geometrical definitions:

1) Bifocal definition.
     - The hyperbola is the locus of a point for which the difference of the distances to two fixed points F and F' is constant in absolute value (see the bifocal equation); hence the following mechanical constructions:
 

Figure taken from the "bible": Lebossé Hémery

The two wires must not slide on one another.

 

Construction by the three-bar mechanism, the length of the two cranks being 2a, and that of the rod 2c; the extensions of the two rods intersect at a point M describing the hyperbola since MF' – MF = MF' – MG' =F'G'= 2a.

This property was applied to the navigation system called LORAN.

The construction of the foci and the directrix of the hyperbola defined as the section of a cone is given by the Dandelin theorem, illustrated below:
 

The two spheres inscribed in the cone and tangent to the plane of the hyperbola are tangent at its foci, and the planes of the contact circles cut the plane of the hyperbola at the two directrices.

1 bis) The hyperbola is the locus of a point M such that the tangent at M to this locus is the internal bisector of the angle F'MF :

The indicated angles are always equal

Applications:

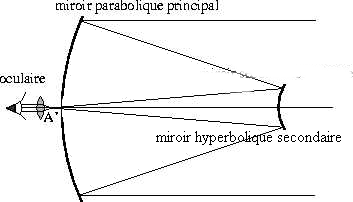
Principle of the Cassegrain reflector

If one aims for the focus of this branch of a hyperbola, the ball will go to the hole after one rebound.

 

Another application: for any point M of the initial hyperbola, the symmetrical hyperbola about the tangent at M is the hyperbola with foci G and G' seen above during the construction with the three-bar. Furthermore, this hyperbola rolls without slipping on the first one.
In the plane linked to F and G, the two hyperbolas turn around F and G while always being tangent, and rolling without slipping: this property is called isotrépence of the hyperbola with respect to a focus.

2) Definition as the equidistance curve between a point and a circle, in other words, as the isotel of a circle.
The hyperbola is the locus of the points at the same distance from a circle (called the directrix circle, with centre one of the foci F' and radius 2a) and a point located outside the circle (which is the other focus F); in other words, it is the locus of the centre of a variable circle constrained to pass by F and be tangent to C(F', 2a).
 

first branch MF = MN (= MF' - 2a ):  the hyperbola is the equidistance curve of the focus F and the blue directrix circle.

second branch MF = MN (= 2a - MF'  )

More generally, the equidistance curves of two exterior circles are reunions of hyperbolas:
 

	The red points are the "equidistant" points of the blue circle and the green one.
		When the circles intersect, the equidistance curve is the reunion of an ellipse and a hyperbola.

3) Tangential definition as the negative pedal of a circle.
The hyperbola is the envelope of the line perpendicular at I to the line (FI), when I describes the principal circle C(O, a) (in other words, the negative pedal of this circle with respect to F), or also the envelope of the perpendicular bisector of the segment line [FN], when N describes the directrix circle C(F', 2a) (which is therefore the orthotomic of the hyperbola with respect to F').

Application: if you draw a circle on a piece of paper, mark a point F outside it, and fold it a certain amount of times by bringing the point F on a point of the circle, theses folds will be enveloped by a hyperbola.

This property is at the base of the elegant construction by the articulated mechanism presented below:

4) Definition by focus and directrix.
The hyperbola is the locus of a point M such that where H is the projection of M on the directrix (D).

     The ratio of the lengths MH and MF is constant (this holds also for the other branch)

This means, if we interpret MF - eMH'  as an optical path length, that if the exterior of the hyperbola is composed of a medium with refractive index n and the interior's index is e.n, then the incident rays parallel to the axis of the hyperbola located on the side of (D') will be refracted as rays passing, all of them, by F. In other words, the caustic by refraction of the hyperbola for rays parallel to the axis reduces to the two foci.

MF'- eMH= 2a, hence

This can be applied to the design of divergent lenses (the refractive index of the lens must be equal to 1/e):

5) Definition as the cissoid of two secant lines:
   Given two secant lines and a point A outside these lines, the locus of the points M such that , where P and Q are the two intersection points between the asymptotes and a variable line passing by A, is the hyperbola passing by A and whose asymptotes are the two initial lines (we derive easily from this that the hyperbola is the cissoid of these two secant curves).

It is this property that is at the base of the following hyperbola-tracers:
 

Hyperbola-tracer of Descartes

Hyperbola-tracer of L'Hospital

Here are also two mechanisms that draw hyperbolas :
 

Hyperbola-tracer of Cavalieri

Hyperbola tracer of Delaunay

6) Definition as the locus of the points for which the product of the distances to two lines is constant.
 

Given two secant lines D and D' forming an angle , the locus of the points for which the product of the distances to D and D' is a constant equal to C² is the reunion of two hyperbolas whose asymptotes are D and D' and whose linear eccentricity is .

Contour lines of the product of the distances to the two blue lines.

Here is also another tangential generalisation:
 

The lines joining two points having uniform circular movements with the same period are enveloped by a hyperbola; this holds for wire tables with circular edge and even for many nails on the edge.

See also on the page of the rectangular hyperbola the construction as the envelope of a triangle.

The evolute of the hyperbola is a half Lamé curve, the equation of which is .

See also the specific page dedicated to the rectangular hyperbola, Gabriel's horn  and the hyperboloids.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  Alain ESCULIER 2017