THREE-BAR LINKAGE CURVE

The curves traced here are half-curves of the three-bar linkage
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
THREE-BAR LINKAGE CURVE

The curves traced here are half-curves of the three-bar linkage
| Curve studied by Chebyshev in 1868, Cayley and Roberts
in 1875, Darboux in 1879 and Koenigs in 1897.
KOENIGS, leçons de cinematiques, Hermann, 1897, p. 246 aa 299 ; BROCARD LEMOYNE T 2 p 116 ; BRICARD, cinematique et mecanismes, A. Colin , 1947 ; H. Lebesgue, Leçons sur les constructions geometriques, 1950 ; ROSENAUER, WILLIS, kinematics of mechanisms, Dover, New York, 1967 ; HUNT, Kinematics, geometry of mechanisms, Oxford University Press, 1978 ; F. RIDEAU, les systemes articules, Pour La science n° 136, fevrier 1989 ; Au dela du compas expos. du Palais de la Decouverte p. 54 aa 57. F. PECAUT : the articulated quadrilaterals See also the website of Alain Esculier for the explanations on the animations on this page. |
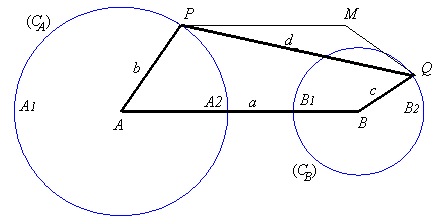
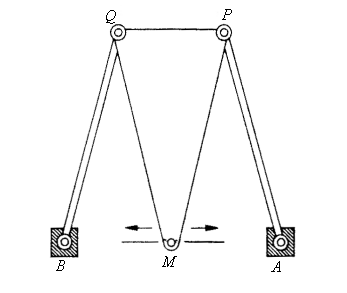
A three-bar linkage curve is the locus of a fixed
point M on the plane linked to the rod [PQ] of an articulated
quadrilateral (APQB), A and B being fixed. The three
"bars" are [AP] and [BQ] (called the cranks or the
rocker
arms) - and [PQ] (called the connecting rod, or the couple).
We choose A(0, 0), B(0, a),
AP
=
b, BQ = c, PQ = d.
 Writing with small letter the affixes of the points, we
have:
|
A curve of the three-bar linkage is therefore the locus of a point linked to a segment line of constant length joining two circles (the circles (CA) and (CB) with centres A and B and radii b and c).
When the cranks have the same length and M is the middle of [PQ], we get a Watt curve.
The curve is not empty if and only if there exists at least a quadrilateral the lengths of the sides of which are a, b, c and d, i.e. iff each of these four numbers is less than or equal to the sum of the others, or also iff
The point P is said to have complete revolution
if it can describe the whole circle (CA)
(same definition for Q); in Mechanics, the arm [AP] is called
a crank when there is complete revolution, and a rocker arm otherwise;
it can be proved that if A1 is the
left-hand intersection point between (CA)
and (AB), and A2 the right-hand
one, then the point P passes by A1
iff and
the point P passes by A2
iff
. The point
P
has complete revolution iff these two conditions are met, and for the point
Q,
there are two similar inequalities obtained by swapping b and c.
The curve is composed of only one component if and only
if, for P and Q, one of the two above inequalities is satisfied(??).
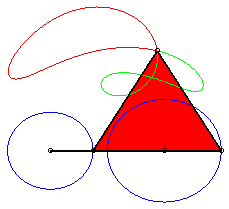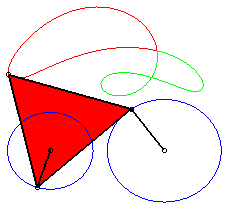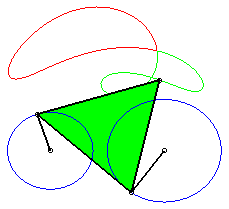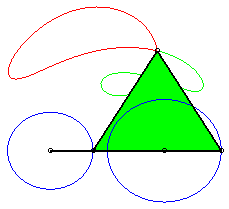
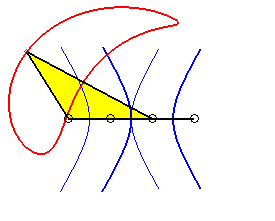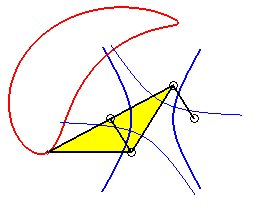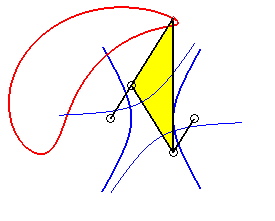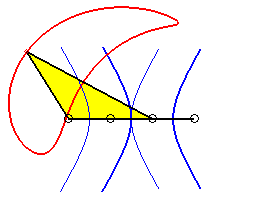
a = 4 ; b =1,5 ; c = 2 ; d = a + c - b ; |
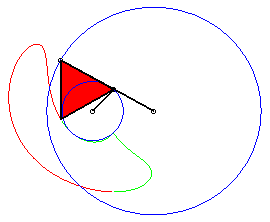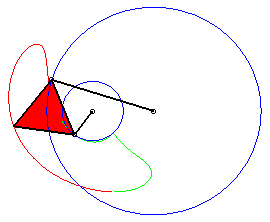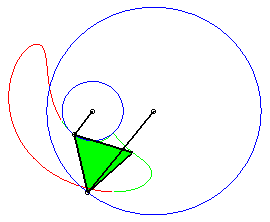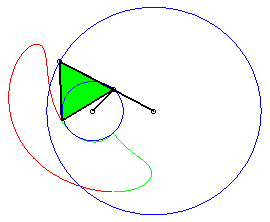
a = 4 ; b =2 ; c = 7 ; d = a ; |
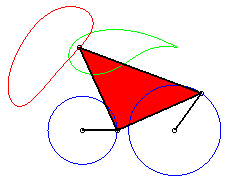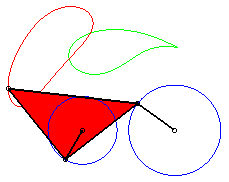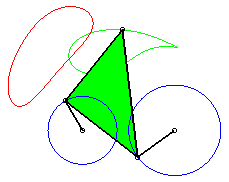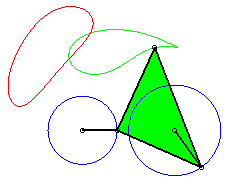 P has complete revolution, but Q does not cross the axis: the curve is composed of two components (that overlap: it is therefore connected!). |
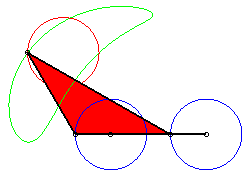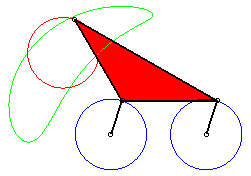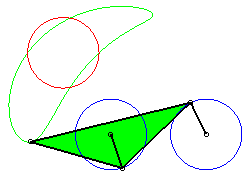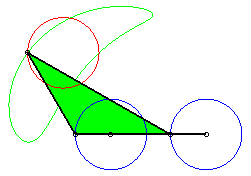  |
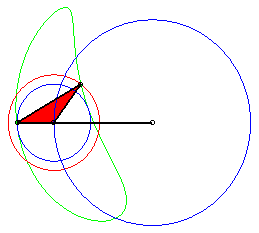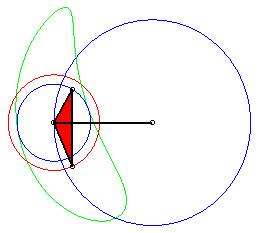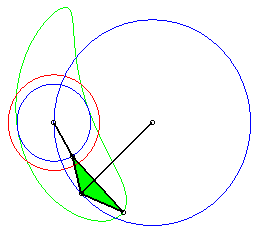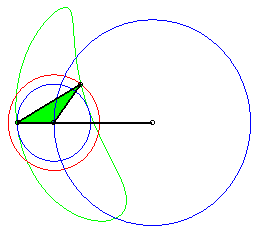
Case of the rhomboid (a = c et b = d) |
The curve is generated by two other ways thanks to two other three-bar linkages [BRSC] and [CTUA] (Roberts theorem of triple generation) :
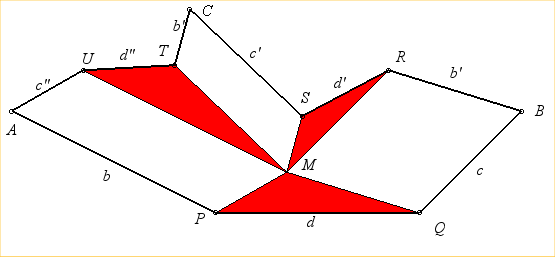 |
The three white quadrilaterals are parallelograms, and
the three red triangles are similar; therefore:
r = b + m – q ; u = a + m –p ; s = r + (m – q)(m – r)/(p – q) ; t = m + (m – q)(m – u)/(q – p) ; c = t + s – m. (b', d', c') is proportional to (d, c, b) and (b" ,d", c") to (c, b, d). The triangle (ABC) remains fixed. |
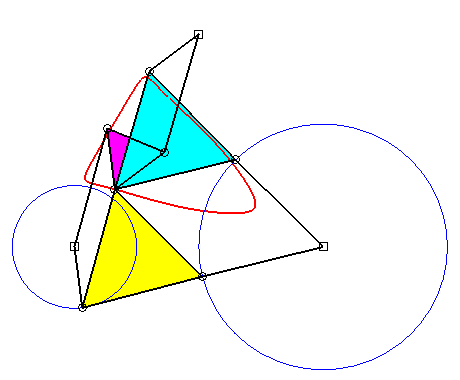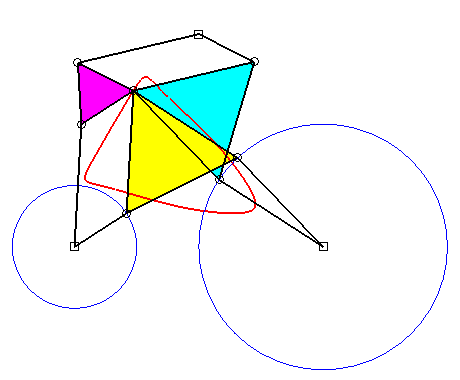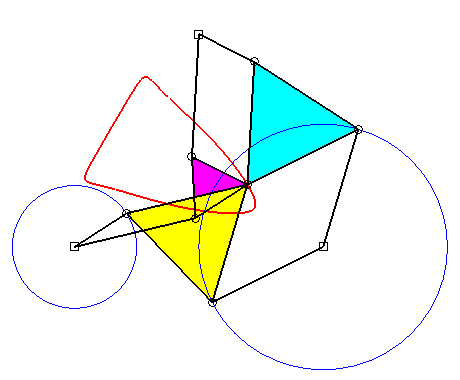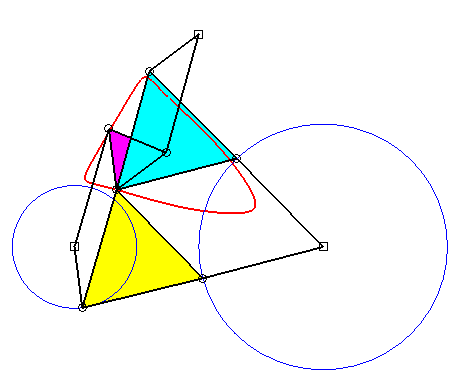 Superb
animation of the triple generation of Roberts due to Alain Esculier.
Superb
animation of the triple generation of Roberts due to Alain Esculier.
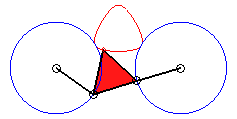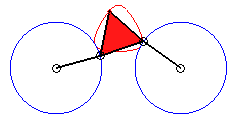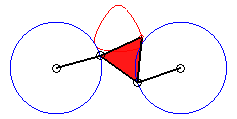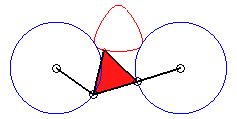
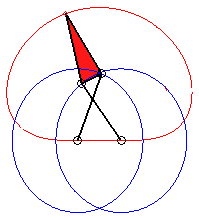
In the case b = c = d and equilateral
triangle (case studied by François Rideau): the triple generation
mechanism has an order 3 symmetry, thus so does the curve; with k
= 3b / a we get the following shapes:
|
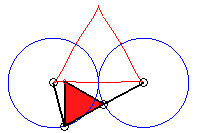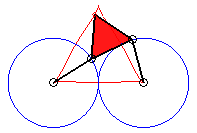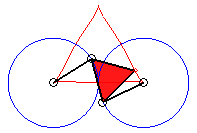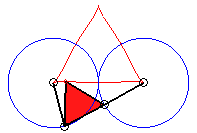
k = 3/2: quasi-triangle |
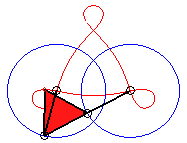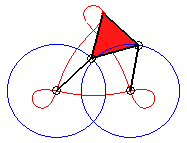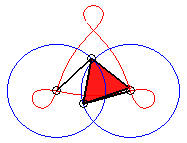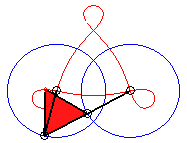
3/2 < k < 3 |
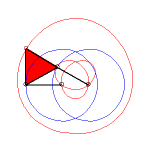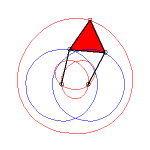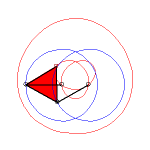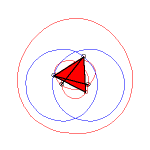
k > 3 |
The case a = 2d, b = c =QM = MP,
corresponds to the Roberts mechanism that provides an almost linear curve
(see also Watt curve).
the curve passes by A, B and the middle of [AB] |
 |
the complete curve (in fact, to be completed with its symmetric image with respect to [AB]) does not have, theoretically, any linear portion. |
Envelope of the rod?
| The curves of the three-bar linkage are special cases of glissettes, when the fixed and sliding curves are circles. | 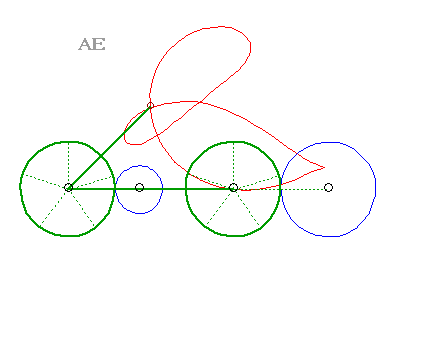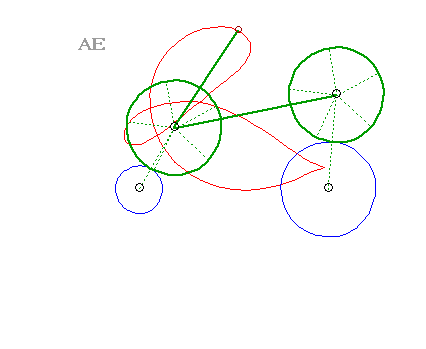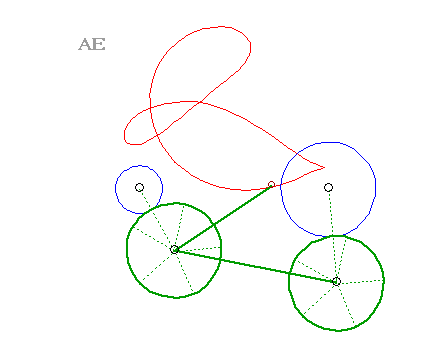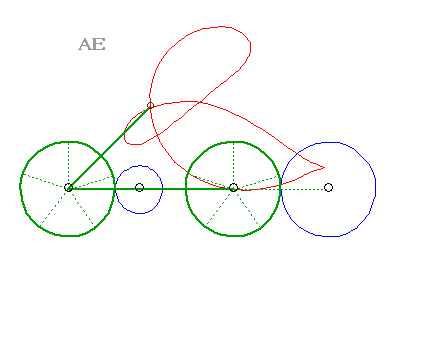 |
These curves can be generalised to the case of a segment line with fixed length (still called connecting rod) the ends of which are constrained to move on two given curves, which also provides a special case of glissette.
When these two curves are non-parallel lines, the points linked to the rod describe ellipses, (La Hire theorem), while the rod envelopes a tetracuspid (?); this mechanism is at the base of the ellipse-tracer of Archimedes.
When one of the curves is a line and the other is a circle, we get the curves of the slider-crank mechanism and, more generally, when one is a line and the other is a conic, we get the polyzomal curves.
Website to visit: php.math.unifi.it/archimede/archimede/curve/geomeccan0.php?id=8
See also the L-system
with three bars and the four-bar
linkage curve.
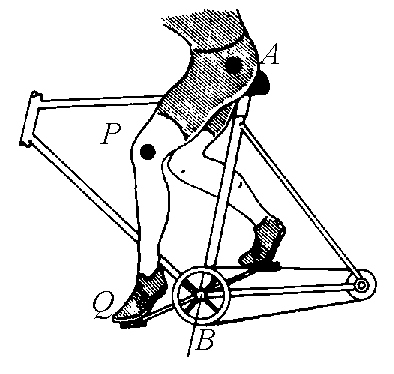 |
 |
| The points on the cyclist's leg describe (in the frame linked to the bike), curves of the three-bar linkage. The points on their thigh describe mere arcs of circles! | The feet of this athlete describe curves of the three-bar linkage. The machine is called elliptic bike, but where are the ellipses? |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL, Alain ESCULIER 2017