FOUR-BAR LINKAGE CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
FOUR-BAR LINKAGE CURVE

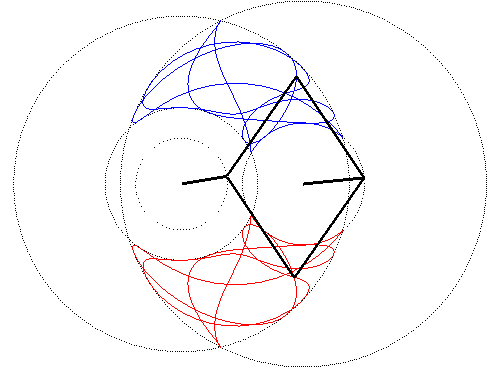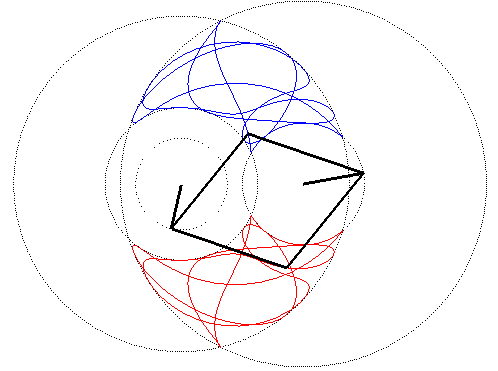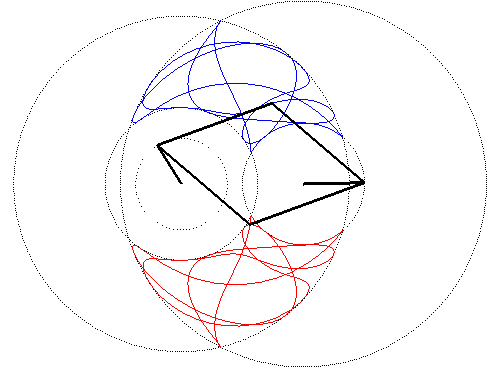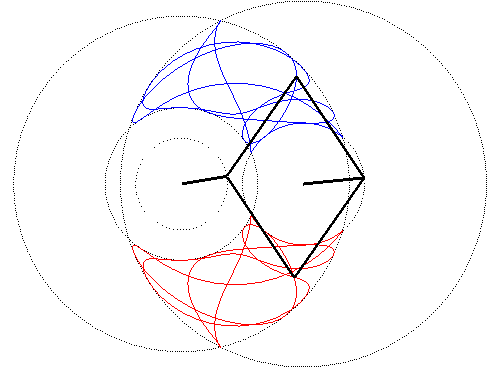
| A four-bar linkage curve is the locus of a point M of an articulated quadrilateral (APMQB), A and B being fixed, P and Q having given motions. The four "bars" are [AP] and [BQ] (the cranks), and [PM] and [QM] (the connecting rods).
With AP=a, BP=b,PM=p and QM=q, the curves are traced in the area delimited by the circles with centres A and radii a+p and a–p, and the circles with centres B and radii b+q and b–q. Above, the cranks have a uniform circular motion, with a = 2b = AB, the ratio of the angular speeds of P and Q being 5/3 and with p = q = 2a. The middle of [PQ] describes a very smooth centred trochoid, in contrast to the chaotic movement of M, even if p = q. |
 |
See also the three-bar linkage curve.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2017