The simplest is the astroid, as well as its affine deformations:

| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
TETRACUSPID
| From the Greek tetra "four" and the Latin cuspis "tip".
Name given by Bellavitis in 1854. Other name: quadricuspid (etymologically more logic...). |
The tetracuspids are the closed curves with 4 cuspidal points.
Here are examples where the 4 cuspidal points are oriented towards the outside of the curve (protruding tetracuspid):
|
The simplest is the astroid, as well as its affine deformations: |
 |
| The evolute of the ellipse |
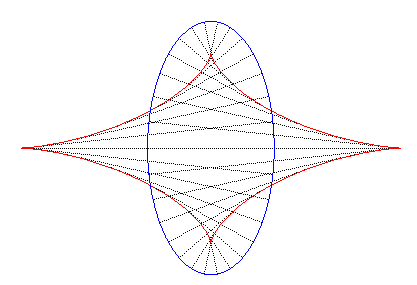 |
Another example, for which the astroid is also a special case, is given by the
JOACHIMSTHAL TETRACUSPID
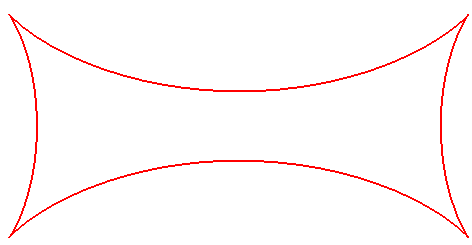
| Problem posed by Merlieux in 1842, solved in 1847 by Joachimsthal. |
The Joachimsthal tetracuspid is the envelope of the line containing a segment of constant length a the ends of which move on two given secant lines.
| If the two secant lines are the lines forming an angle Cartesian parametrization: Rational sextic. |
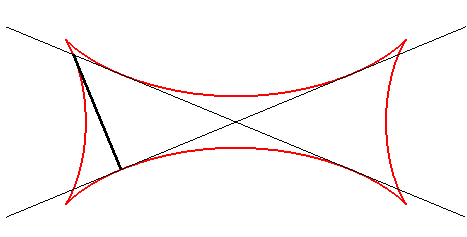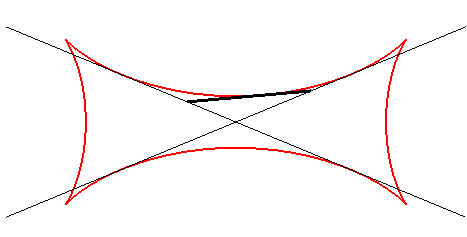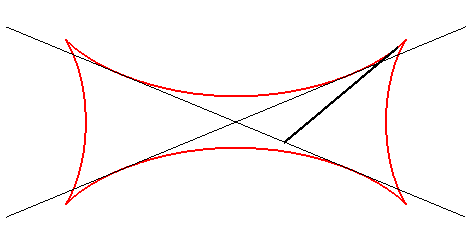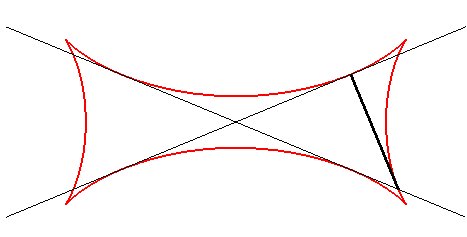
The points on the moving line describe ellipses. |
Other protruding tetracuspids:
- The Maltese cross.
- some toroids
- some reptorias of ellipses
Here are examples where the 4 cuspidal points are oriented towards the inside (huddled tetracuspid):
| The epicycloid with four cusps: |
 |
| The family of curves parametrized by: Opposite, the case n = 5: |
 |
| It so happens that the case n = 3 can be obtained as the orthoptic of the cross curve: |
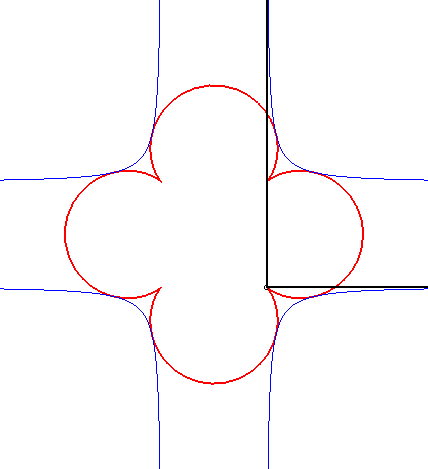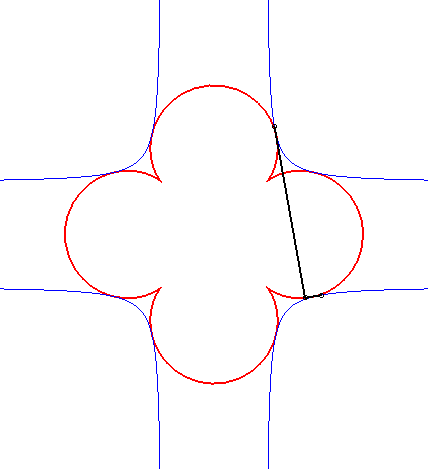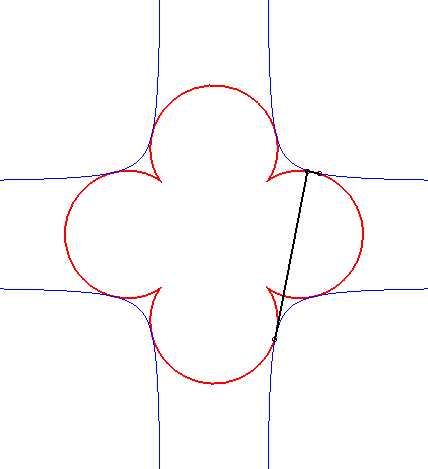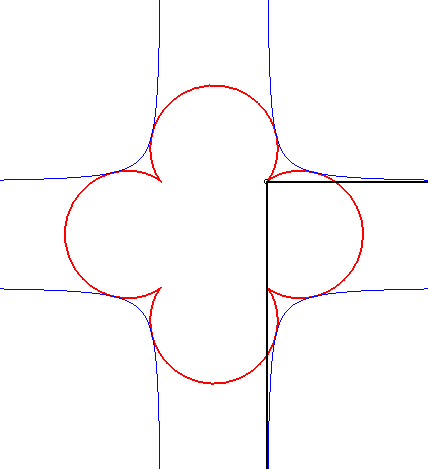 |
| The Cartesian equation of the previous curves is Opposite, the case |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017