The orthoptic (curve) is the locus of the points by which pass two perpendicular tangents to the curve, in other words, the locus of the points from which we "see" the curve under a right angle; it is therefore a special case of isoptic curve.

Examples:

    - The orthoptic of the parabola is its directrix.
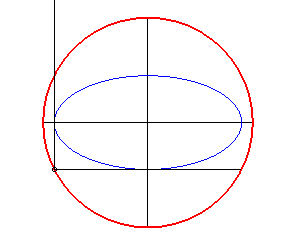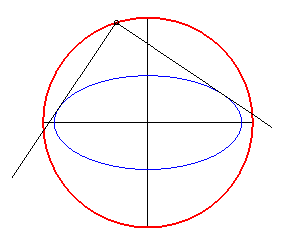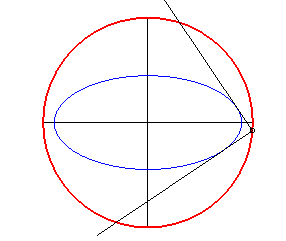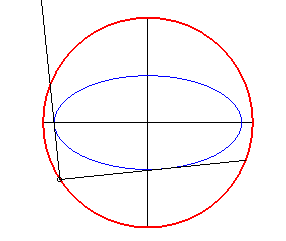
    - The orthoptic of a centred conic with eccentricity less than is a circle, called orthoptic circle or Monge circle. For the ellipse, it is the circle with centre O and radius  (circumscribed to its rectangle). For the hyperbola, it is the circle with centre O and radius .

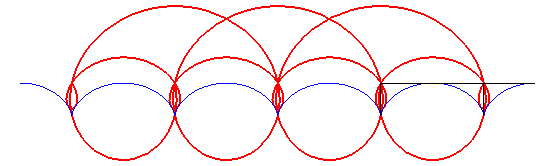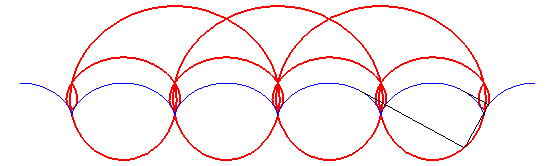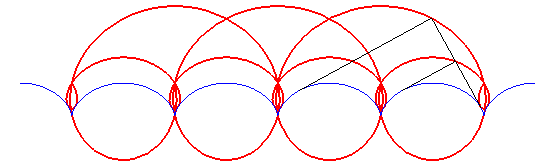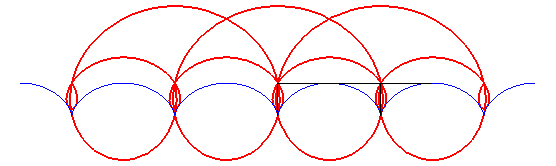
    - The orthoptic of the cardioid is the reunion of a circle and a limaçon of Pascal with a loop, with (see the animation above).

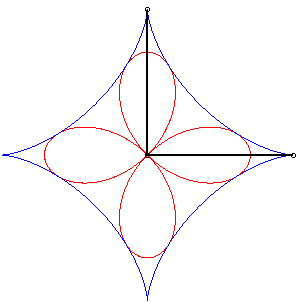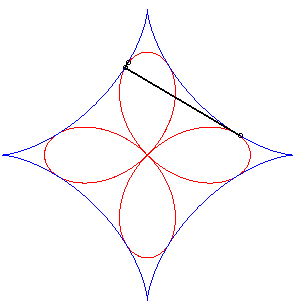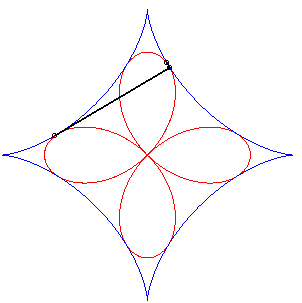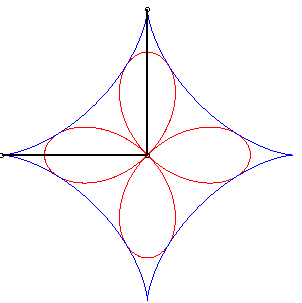
    - The orthoptic of the deltoid is its inscribed circle.
 
 

	-
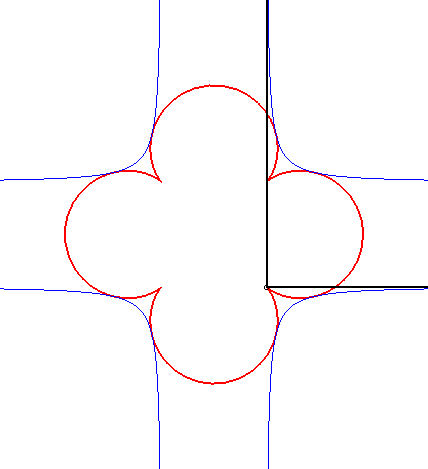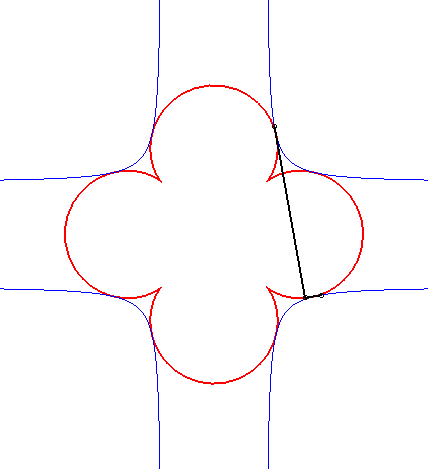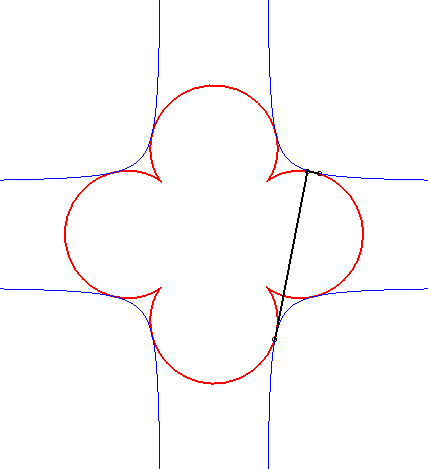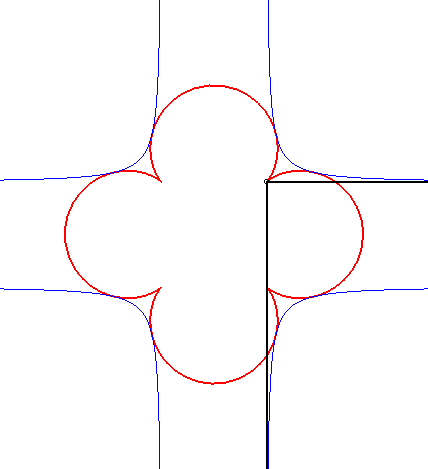- the orthoptic of the astroid is a quadrifolium.	- the orthoptic of the cross curve is a beautiful curve with 4 cusps (see tetracuspid).

    - more generally, the orthoptic of a trochoidal curve is the reunion of trochoidal curves.

    - the orthoptic of a logarithmic spiral is a logarithmic spiral.

    - the tractrix is the orthoptic of the reunion of two logarithmic curves.

    - the orthoptic of the Maltese cross is the cornoid.

   - the pedal of a curve can be considered as the orthoptic of the reunion of this curve and a point.

Other examples Broc comp p. 134.

The orthoptic of the evolute of a curve is the locus of the points by which pass two perpendicular normals to the curve.

A similar notion, bearing the same name, is that of orthoptic of a part X of the plane: locus of the vertices of the right angular domains circumscribing X (that is to say: containing X and both sides of which intersect with X). The orthoptic of the cardioid drawn at the top of this page is then only composed of the external part of the red curves.

See the notion of orthoptic surface.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017