Logarithmic curve

LOGARITHMIC CURVE

Other name: exponential curve.

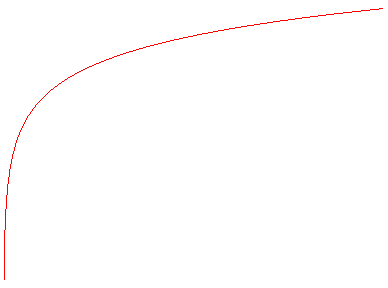
Logarithmic version:
Cartesian equation: .
Transcendental curve.
In the case where a = b:
Curvilinear abscissa starting from the point with abscissa a:

The Cartesian tangential angle is defined by .
Radius of curvature: .

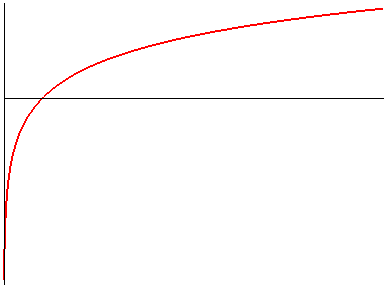Exponential version:
Cartesian equation: .
Transcendental curve.
In the case a = b:
Curvilinear abscissa starting from the point with zero abscissa:
.
The Cartesian tangential angle is defined by .
Radius of curvature: .

The logarithmic curve is the plot of the logarithmic function (and also that of the exponential function) or its image by a dilatation.

NSC: curve with constant sub-tangent.

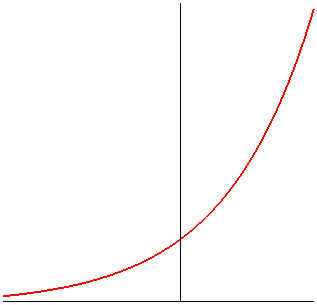
The logarithmic curve is also characterized by the fact that translating it along its asymptote is equivalent to scaling it perpendicularly to this asymptote.
Translation equivalent to a scaling in one direction

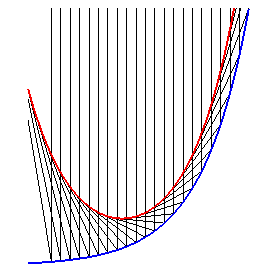
In the case where a = b, its caustic by reflection for rays perpendicular to its asymptote is the catenary.
For rays parallel to the asymptote, it is a pursuit curve.

The logarithmic curve is the profile a tower (i.e. a solid of revolution) must have in order for the pressure applied on any horizontal section by the upper section to be constant.
See tower of constant pressure.

Logarithmic version: Cartesian equation: . Transcendental curve. In the case where a = b: Curvilinear abscissa starting from the point with abscissa a: The Cartesian tangential angle is defined by . Radius of curvature: .
Exponential version: Cartesian equation: . Transcendental curve. In the case a = b: Curvilinear abscissa starting from the point with zero abscissa: . The Cartesian tangential angle is defined by . Radius of curvature: .