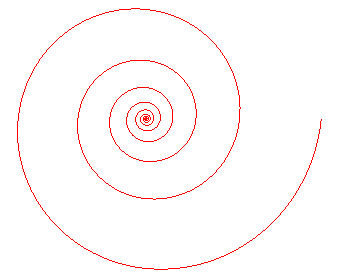
LOGARITHMIC SPIRAL
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
LOGARITHMIC SPIRAL

| Curve studied by Descartes and Torricelli in 1638, then
by Jacques Bernoulli (1654-1705).
Other names: equiangular spiral, Bernoulli spiral, spira mirabilis; the name "logarithmic spiral" was given by Varignon. Jacques Bernoulli had a logarithmic spiral engraved on its gravestone in the Basel Munster, with the epigraph: eadem mutata resurgo, "although changed (mutata), I arise (resurgo) the same (eadem)". Nonetheless, the engraver traced an Archimedean spiral... |
 |
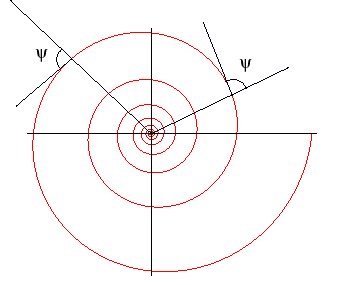 |
Polar equation: Complex parametrization: Transcendental curve. Curvilinear abscissa and intrinsic equation 2: Radius of curvature: Intrinsic equation 1: Intrinsic equation 2: Pedal equation: |
The logarithmic spiral can be defined as
- the curve the polar tangential angle
of which
remains constant (different from a right angle)
- the curve the curvature of which
is inversely proportional to the curvilinear abscissa
- the curve the radius of curvature
of which is inversely proportional to (and greater than) the radius vector
( with l
> 1)
Therefore, the logarithmic spirals with centre O
are the trajectories at angle.
of the pencil of lines issued from O.
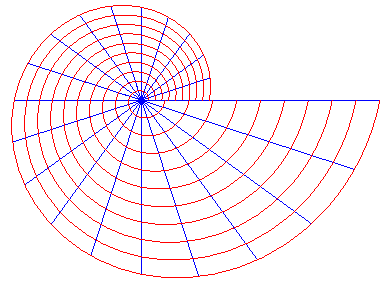
The logarithmic spiral is also the stereographic projection
from the south pole of the rhumb
lines of the spheres with centre O, forming an angle
with the meridians (since the stereographic projection is a conformal map).
Finally, it is the planar expansion of an helix of a cone of revolution.
The logarithmic spiral has an exceptional stability with respect to the classic geometrical transformations:
- any rotation with centre O
and angle
of the spiral amounts to a homothety with same centre and ratio
,
which in turn amounts to the identity if
.
Rotation equals homothety! |
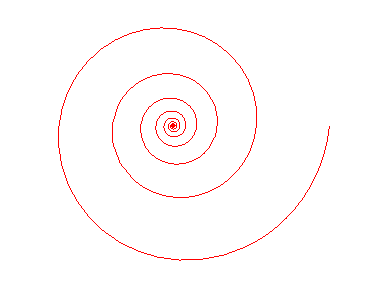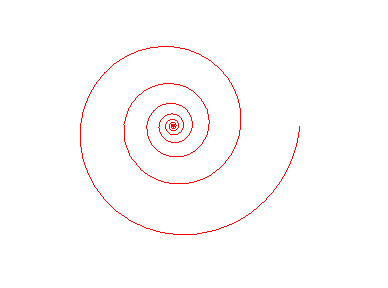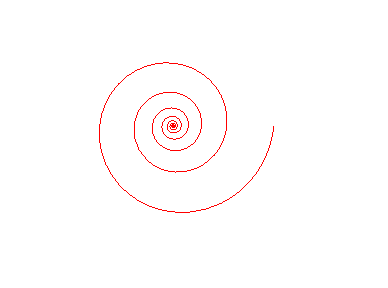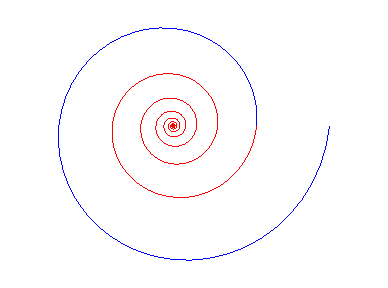
Homothety equals identity! |
- any inversion with centre O
amounts to a reflection about an axis passing by O.
- its evolute
is a logarithmic spiral with same centre and same angle(and,
besides, the limit of the n-th evolute of any curve is a logarithmic
spiral).
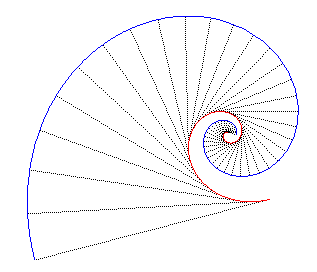
- its caustics by reflexion or diffraction, when the light source is at O, are logarithmic spirals.
- the mating gear associated to a gear shaped like an logarithmic spiral is an isometric logarithmic spiral.
When a logarithmic spiral rolls on a line, the asymptotic point describes another line:
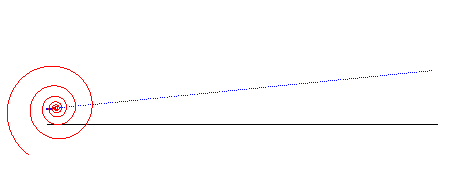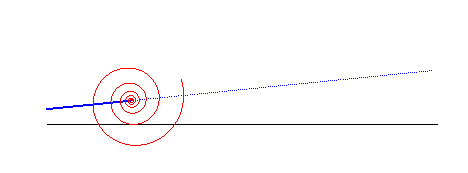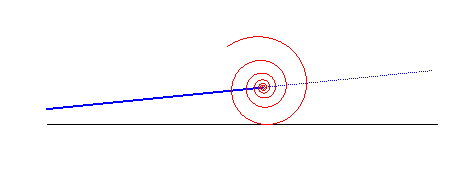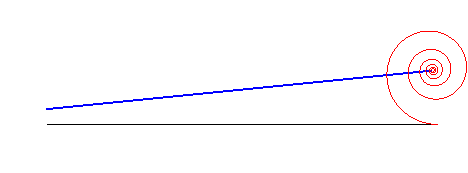
The logarithmic spiral is a solution to the three following physical problems:
1) The force centred on O that
makes a point in space describe a logarithmic spiral is proportional to
1/r3 (this force,
according to the Binet formula, is proportional to
which, here, is equal to
,
with u = 1/r).
2) the curve (called brachistochrone)
that minimises the travel time of a point moving freely along this curve,
when it is itself turning around a fixed centre O at constant speed,
in the case where the speed of the moving point vanishes at O, is
a logarithmic spiral.
3) A particle of mass m1
and charge q placed in a uniform magnetic field of intensity B
with a speed v0 perpendicular to
the field describes a logarithmic spiral with
and
.
see: perso.libertysurf.fr/hdehaan/mecanique/M6/M6_2/M6_2_cadre.htm
| If u is a complex number different from 0, then
the image points of the geometric sequence Opposite, u = 1+i/4. |
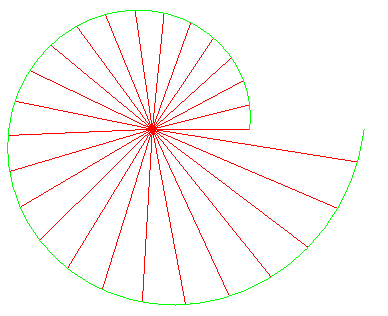 |
| In the same way, any sequence points of polar coordinates For example, on the opposite figure, the points with polar
coordinates ((1,1)k ; (k+2l)p/n)
were traced, in blue if l is even, in red otherwise. These points
are placed in a quincunx pattern at the intersection between concentric
circles with radii in geometric progression and concurrent lines; but they
are also located on the logarithmic spirals with equation |
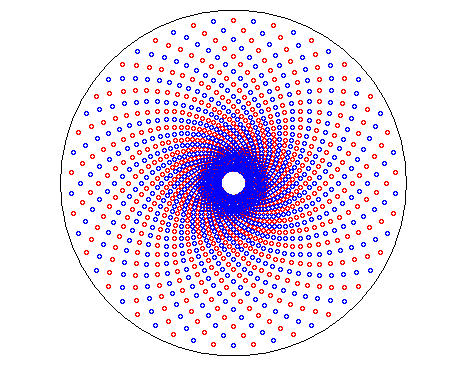
|
 |
Here, the same spirals, but coloured in triangles in the style of this mosaic which adorned a Roman villa in Corinth in the 2nd century AD. |  |
| Furthermore, as it could be noticed on the previous figures,
the spirals |
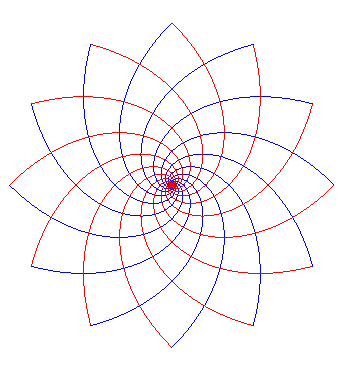 |
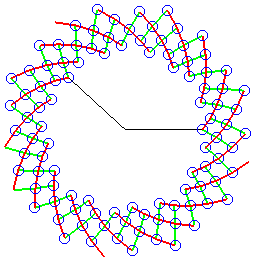
| Phyllotaxis
The scales of pine
cones develop on a logarithmic spiral in such a way that the angular
difference (in relation to the centre) between two consecutive scales is
the golden angle
equal to |
 |
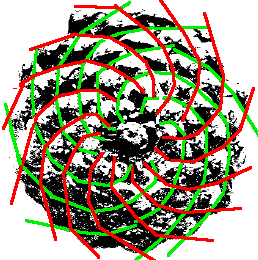 |
|
View of points of polar coordinates On the view secondary spirals. On the picture where the scales are indicated with the appearance number, we note that the k-th secondary spiral is associated with The scales of the k-th secondary spiral associated with Note: the angle between two red and green spirals that
intersect is constant but not related to the golden angle as we sometimes
see written, since it depends on the value of r!
|
 |
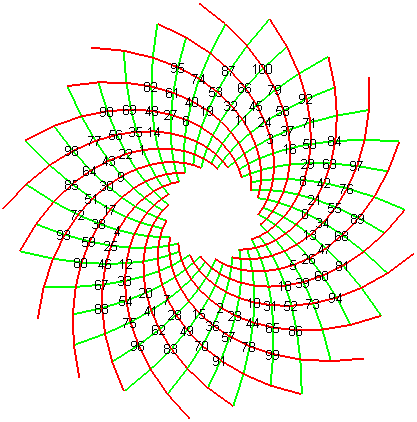 |
| If we increase the ratio r to 1.02, it is rather
the 8 = These secondary spirals associated with the Fibonacci numbers appear visually because multiplying the golden angle by the terms of the Fibonacci sequence yields results the moduli of which approach zero for large n: we can see clearly in the figure where the scales are indicated with their number of appearance that the fibonaccian scales 3, 5, 8, 13, 21, 34, 55, 89 are close to the x axis. On this page, we can test different angles of rotation between two sunflower florets and note that the arrangement of the florets is optimal in the case of the golden angle. See also this numberphile video.
|
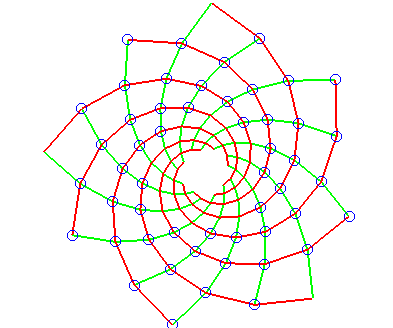 |
 |
If we consider a sequence of concurrent lines D1,
D2,
.... each of them forming an angle e with the next one, and so that
if, starting from M1 on D1,
M2
on D2 is defined so that the angle
between D1 and M1M2
is equal to ,
and M3,
M4,
... are defined in the same way, then the moduli of the points Mn
are in geometric progression with common ratio
and their arguments are in arithmetic progression with common difference
e,
and thus are on a logarithmic spiral with
;
it can be checked that
goes indeed to cot
as
goes
to 0, so that the spiral corresponding to
goes
to the logarithmic spiral with k = cot
.
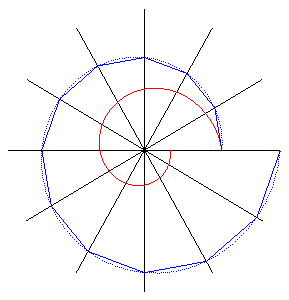
here, y = 100°, e = p/10. |
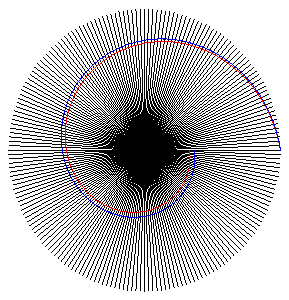
here, y = 100°, e = p/50. |
REMARK: when
= 90°, Mi+1
is defined so that Mi
is its orthogonal projection on Di
(careful not to mistake it with the Theodore
spiral which is an approximate Archimedean
spiral).
Another approximate construction consists in taking arcs
of circles with constant angles
and radii in geometric progression with common ratio
,
with tangential connection.
For a very beautiful special case, see the
golden
spiral.
The spiral traced on a cone which is projected on a logarithmic
spiral is the conical
helix.
See also the spiral of the rotating rod and the mutual pursuit curves.

Ceiling of a room in the Pavlovsk Palace in Saint Petersburg
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2019