| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CAUSTIC
|
|
|
| Notion studied and named by Tschirnhausen
in 1681 and then by Jacques Bernoulli in 1691, and La Hire in 1703.
From the Latin causticus, copy of the Greek kaustikos: burning. |
The word caustic refers, in a general fashion, to the envelope of light rays emitted from a finite distance (the source is then called the radiant) or an infinite one after they are modified by an optical instrument. Every modified ray is considered as a whole, and includes the virtual ray.
A) CAUSTIC BY REFLECTION
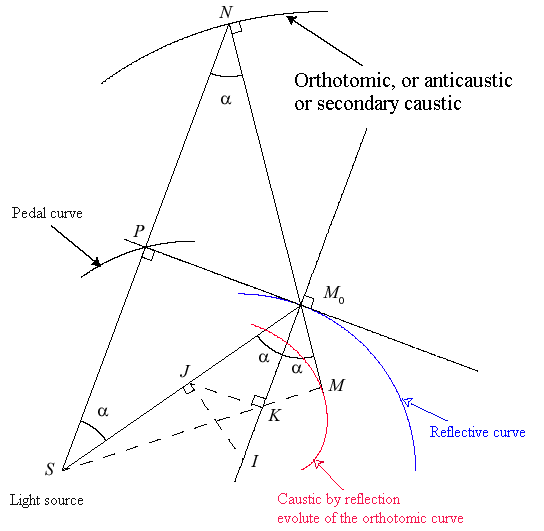
In a plane, the caustic by reflection (or catacaustic)
of a curve 
with respect to a light source S is the envelope of the rays emitted
by S after reflection on a mirror with profile .
I) Case where S is a radiant.
In this case, the caustic by reflection of the reflecting
curve
is the evolute of the orthotomic,
who is, then, rather called anticaustic or secondary caustic.
Recall that this curve is itself the homothetic image with centre S
and radio 2 of the pedal of
with respect to S.
 |
|
 |
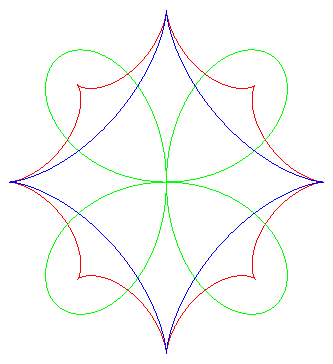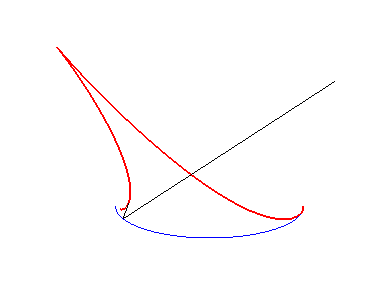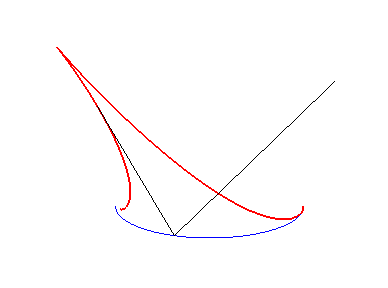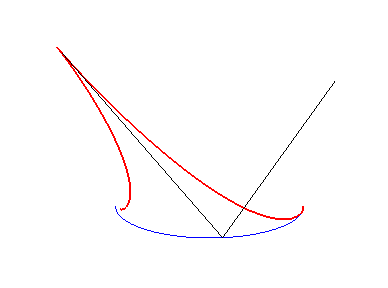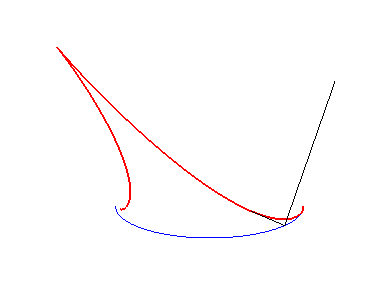
| Construction of the characteristic point M on the reflected ray: the centre of curvature I at M0 is projected on J on the incident ray, then on K on the normal at M0. S, K and M are aligned. | The red caustic is the evolute of the green orthotomic of the blue ellipse. | The red caustic is the evolute of the green orthotomic of the blue astroid. |
Application of this result: the caustic by reflection of the negative pedal of a cycloidal curve is a similar cycloidal curve.
Examples:
| reflecting curve | light source | caustic by reflection |
| circle | on the circle and at the top of the cardioid | cardioid |
| circle | any point
pole of the limaçon |
caustic of a circle |
| parabola | focus of the parabola | reduces to a point at infinity in the direction of the parabola |
| bifocal conic | focus of the conic | reduces to the other focus |
| logarithmic spiral | asymptotic point of the spiral | logarithmic spiral |
| Tschirnhausen cubic | focus | semicubical parabola |
| cissoid of Diocles | point (4a, 0) | cardioid |
| cardioid | cuspidal point | nephroid |
| inverse caustic of a circle | centre | circle |
II) Case where S is at infinity.
In this case (the incident rays are parallel), the caustic can also be defined as an evolute. Given a line D orthogonal to the rays, the caustic is the evolute of the anticaustic associated to the line D, locus of the symmetrical image of the projection of M0 on D about the tangent at M0. Note that the various anticaustics associated with the lines D are parallel and therefore have the same evolute.
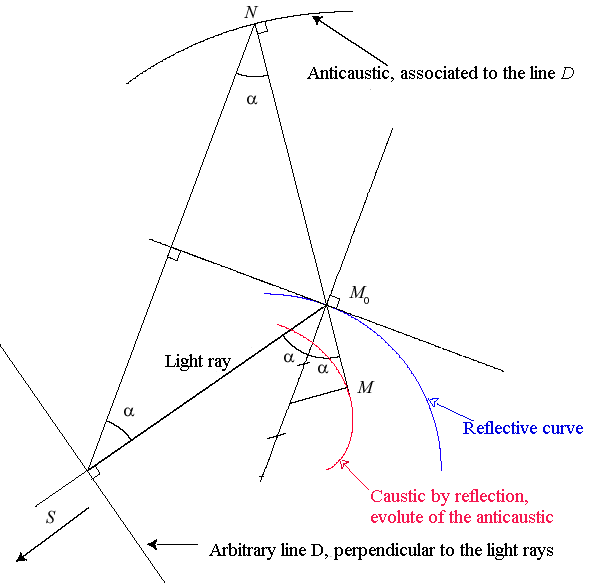
Cartesian parametrization for rays parallel to Ox:  |
Examples:
| reflecting curve or
inverse caustic |
direction of the rays | caustic |
| circle | any direction | nephroid (curve of the coffee cup) |
| parabola | parallel to the axis | focus |
| parabola | any other direction | Tschirnhausen cubic |
| cubic parabola ay2=x3 | parallel to Oy | Tschirnhausen cubic |
generalised parabola 
(  ; the case
k=1/2
corresponds to the previous case) |
parallel to Oy | pursuit curve
(k = speed of the master / speed of the dog) |
| logarithmic: y = a ln (x/a) | parallel to Oy | pursuit curve
(speed of the master = speed of the dog) |
| arch of a cycloid | perpendicular to the axis of the rolling motion | two arcs of a cycloid reduced by half. |
| deltoid | any direction | astroid |
| exponential
y = a ex/a |
parallel to Oy | catenary |
B) CAUSTIC BY REFRACTION (generalises the previous case)
The caustic by refraction (or diacaustic)
of a curve
with respect to a light source S is the envelope of the rays emitted
by S after refraction on a dioptre with profile
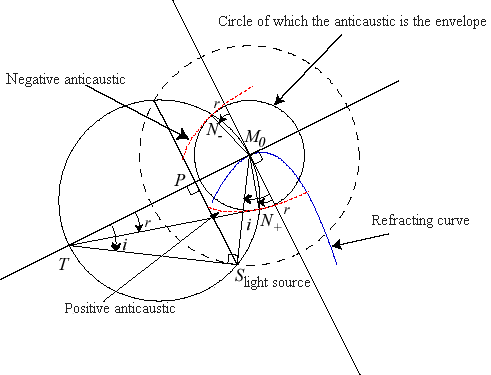
If M0
is a point on the curve
and n a constant (that can be negative), the refracted ray associated
to the incident ray (SM0)
is the line (D) such that r is the angle formed between (D)
and the normal (N) to
at M0, with 
,
where i is the angle 
.
Only the case n > 0 corresponds to the physical
refraction (n is then the ratio 
of the refractive indices in the side to which S does not belong
and the one to which it does); the case n = –1 corresponds to the
reflection.
The reunion of the caustics for the constants n
> 0 and –n is referred to as complete caustic by refraction
for the constant n. It is the evolute of the anticaustic
of with
respect to S associated to the constant n.
Examples:
- the complete caustics by refraction
of the straight line are the evolutes of conics and the complete caustics
by refraction of the circle are the evolutes of complete Cartesian
ovals.
- the curves for which the caustic
by refraction reduces to a point are the conics for parallel incident rays,
and the Cartesian ovals for
a radiant.
See also on this page the example of the caustics by refraction of circles, for a light source at infinity.
C) ORTHOCAUSTIC.
The orthocaustic of
with respect to a light source S is the envelope of the lines perpendicular
to the rays emitted by S at their point of impact on .
The orthocaustic is therefore none other than the negative
pedal.
Examples: the orthocaustic of a straight line (D) is the parabola with focus S and tangent to (D); the orthocaustic of a circle (C) is the ellipse or hyperbola with focus S and bitangent to (C).
D) OTHER CAUSTICS.
For a pool table delimited by a convex curve, the envelope
of the consecutive trajectories of a pool ball (in the case where this
trajectory is not periodic) is also referred to as "caustic". For example,
for an elliptic pool table, the caustic is an homofocal ellipse or hyperbola
(see this
site).
See also, in the field of curves defined by optical means,
the anamorphoses.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017
