Nephroid

NEPHROID

Curve studied by Huygens, Tschirnhausen in 1679, Jacques Bernoulli in 1692, Daniel Bernoulli in 1725 and Proctor, who named it in 1878.
From the Greek nephros "kidney".

Complex parametrization: .
Cartesian parametrization: .
Cartesian equation: .
Rational sextic.
Polar equation: .
Curvilinear abscissa: .
Cartesian tangential angle: .
Radius of curvature: .
Intrinsic equation 1: .
Intrinsic equation 2: .
Pedal equation: .
Length: 12 a; area: 3pa².

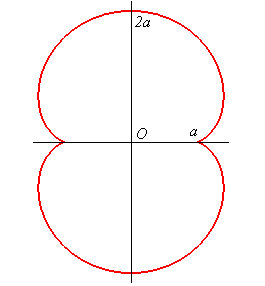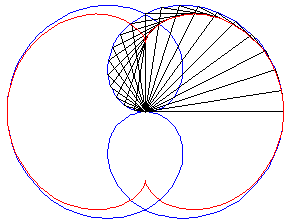
The nephroid is an epicycloid with two cusps (circle with radius a/2 rolling outside a circle (C) with radius a).

It is also
- a pericycloid (circle with radius 3a/2 rolling on the circle (C), and containing it):

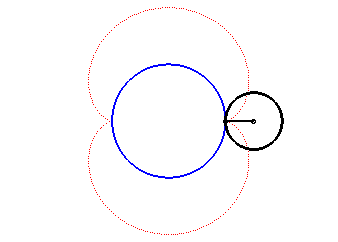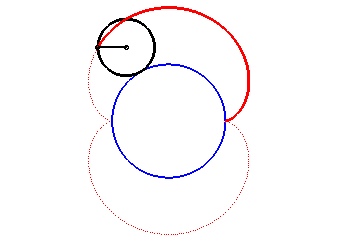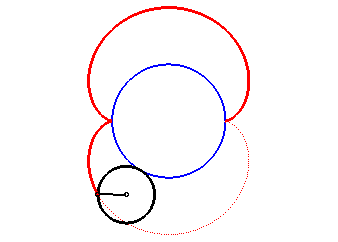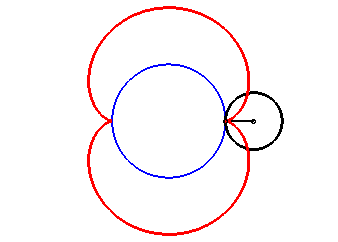
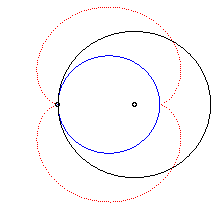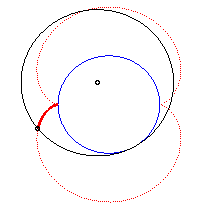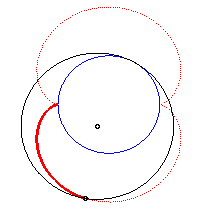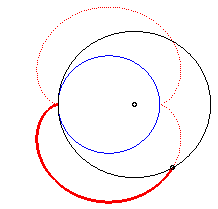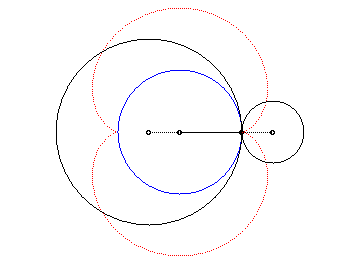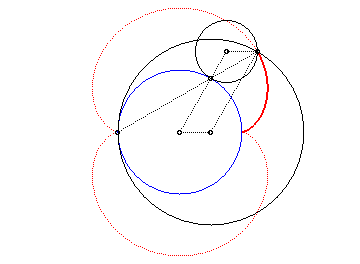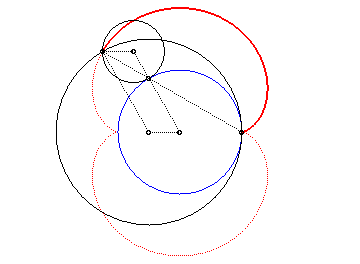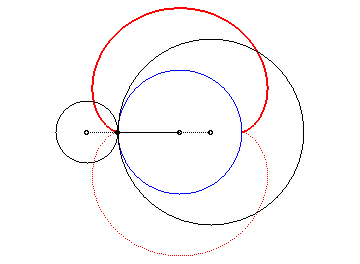
Animation of the double generation

- the envelope of a diameter of a circle with radius a rolling without slipping on (C) externally.

- the envelope of a chord (PQ) of the circle with centre O and radius 2a (circumscribed circle of the nephroid), when P and Q travel along the circle in the same direction, the speed of one being three times the speed of the other (Cremona generation).

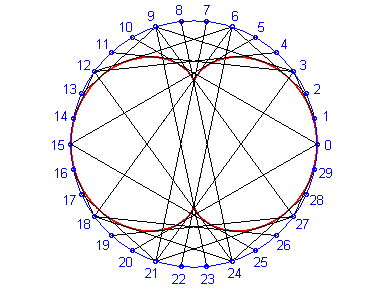
Above, the points n and 3n modulo 30 are linked.

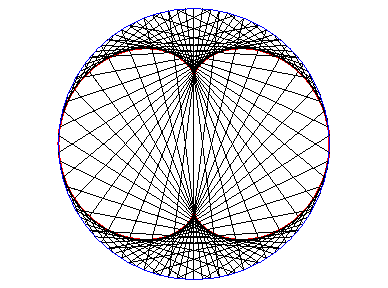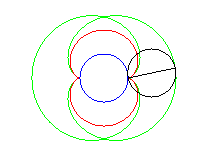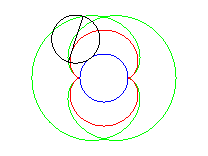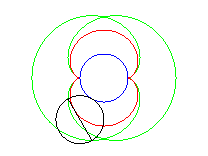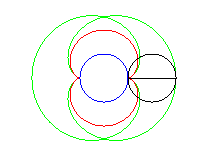
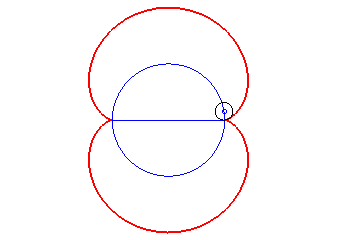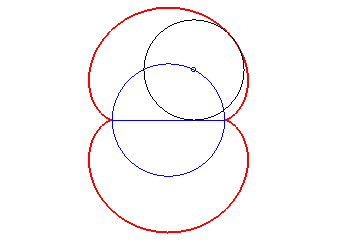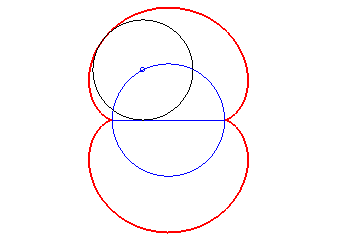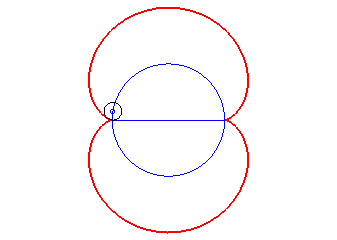
The nephroid is also:
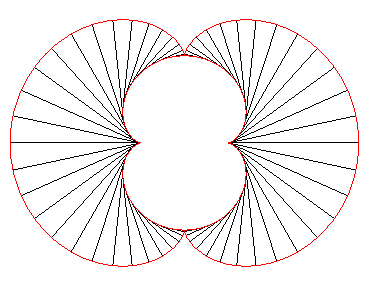
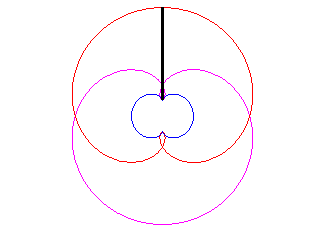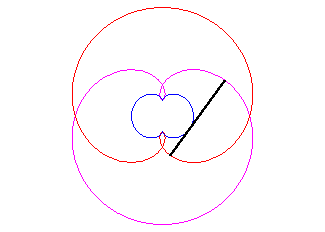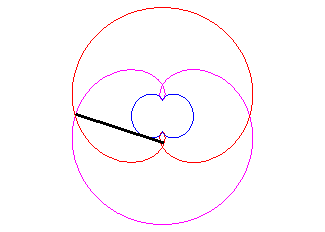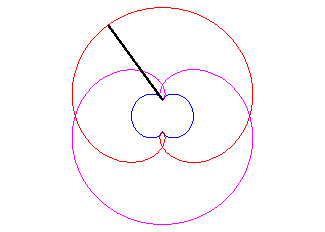
- the envelope of the circles centred on a circle (here, (C)) and tangent to one of its diameters (here Ox). The nephroid is therefore the symmetric image of a diameter with respect to this circle.

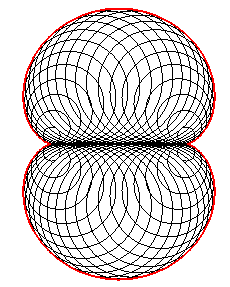
- the caustic by reflexion of a circle (here, (C)) with a light source at infinity (here, the incident rays are parallel to Ox).

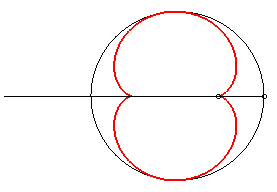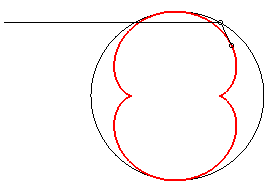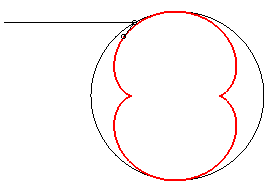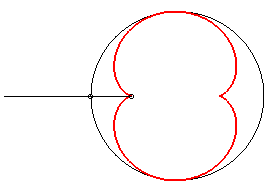
It is because of this property that the half-nephroid appears in your coffee cup, or here in an enamel plate.

See also cardioid.

- the caustic by reflection of the cardioid, with the light source at the cuspidal point of the cardioid. Therefore, it is also the evolute of the Cayley sextic, which is its orthotomic (or its pedal).

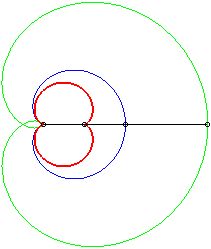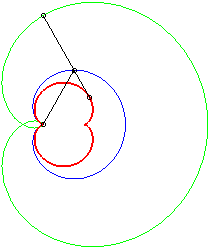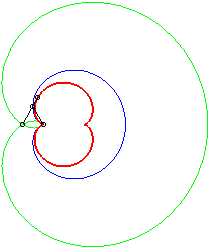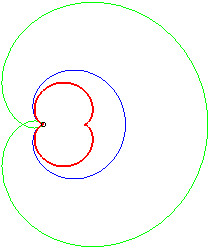
- the negative pedal of the rose r = 2a sin q/2:

Like all cycloidal curves, its evolute is a similar curve, image by the similarity with centre O, radius 1/2 and angle p/2.

One of the involutes is therefore a nephroid; here are two others:

The real kidney has only one symmetry axis...