NODAL CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
NODAL CURVE

| Curve studied by La Gournerie in 1851. |
| Polar equation: |
The nodal curves are the Brocard transforms of the Kappa, when the pole is at the centre of the Kappa.
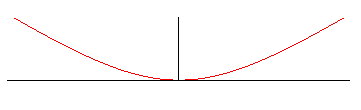
Each curve is composed of an infinite branch, the base, obtained for 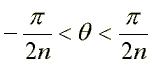
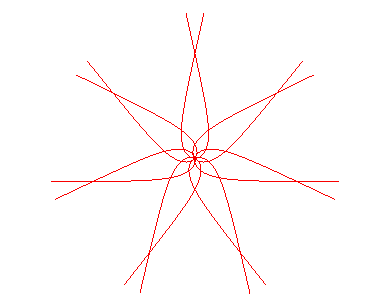
If n is rational and its numerator is p and its denominator q, then the curve is composed of 2p branches, images of the base branch by rotation when q is odd, and p branches when it is even.
Examples:
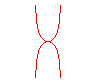
n = 1 : Kappa |
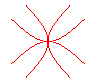
n = 2: windmill |
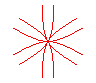
n = 3 |
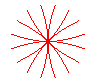
n = 4 |
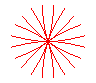
n = 5 |

n = 1/2: right strophoid |

n = 3/2 |
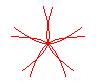
n = 5/2 |
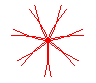
n = 7/2 |
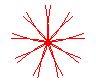
n = 9/2 |
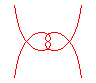
n = 1/3 |
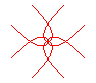
n = 2/3 |
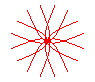
n = 4/3 |
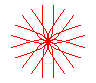
n = 5/3 |
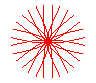
n = 7/3 |
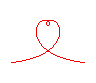
n = 1/4 |
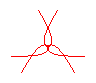
n = 3/4 |
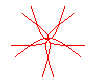
n = 5/4 |
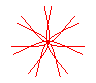
n = 7/4 |

n = 9/4 |
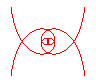
n = 1/5 |
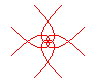
n = 2/5 |
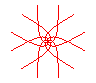
n = 3/5 |
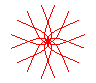
n = 4/5 |
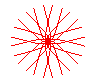
n = 6/5 |
All nodal curves are stereographic projections of the clelia.
The inverse (with centre O and radius a2) of a nodal curve is the same curve turned by .
Asymptotic line of a 3D helicoid????
Compare to the epispiral.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017