Kappa

KAPPA

Curve studied by Gutschoven in 1662, Barrow in 1672, and Sluse in 1862.
Other names: Gutschoven curve, tangentoid spiral.
Kappa: name of the Greek letter k, in fact the curve looks more like an x.

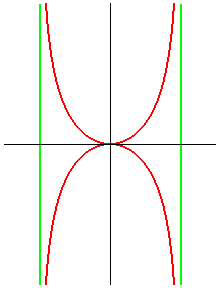Polar equation:

(or

if we want the curve to look like an x)
Cartesian equation:

that can be written

.
Cartesian parametrization :

.
Rational quartic.
Area of the domain between the curve and its two asymptotes: pa².

The Kappa is the locus of the vertex M of a set square zMB the side (zM) of which passes by O, while the vertex B slides on the line Oy .

In this sense, the Kappa is a glissette with bases O and Oy and sliding curves Oz and B (see the page glissette, special case n°5).

Other construction, equivalent to the previous one: the Kappa is the locus of the vertex M of a right triangle at OPOM, when P describes the circle with centre O and (PM) remains parallel to a fixed line. This construction is a limit case of the construction of a curve as the locus of the orthocentre of a triangle with fixed base (here, reduced to the point O) while the vertex (here P) describes a given curve, see for example the construction of the bicorn.

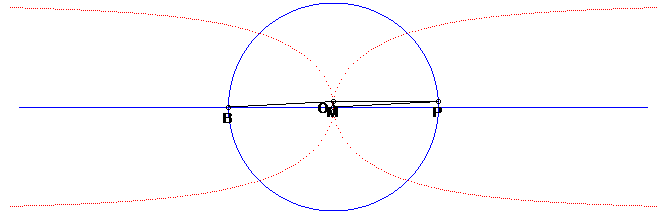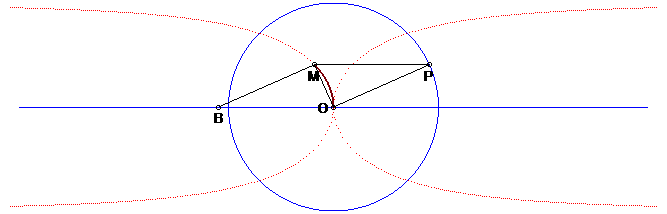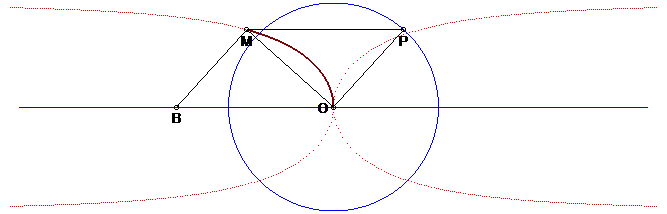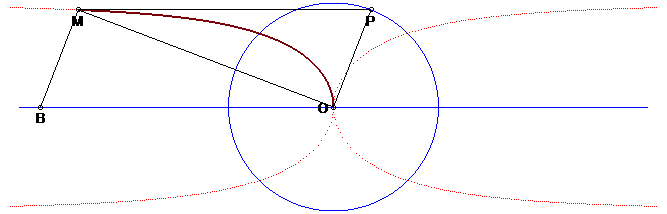Third construction: given a variable line (D) passing by O and cutting the line x = a at N, the Kappa is the locus of the points M on (D) such that OM = AN where A(a,0).

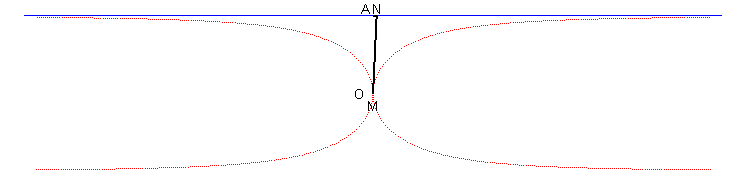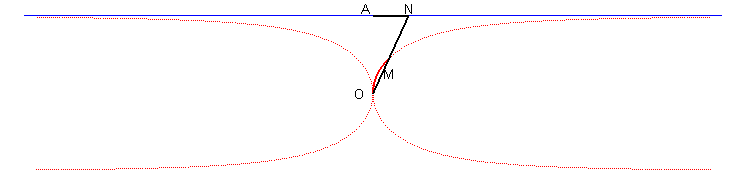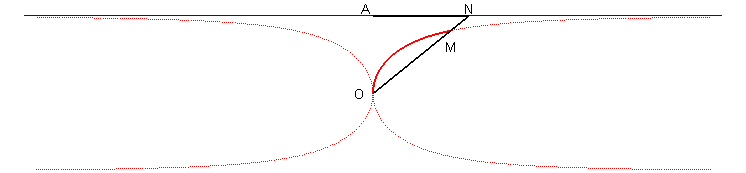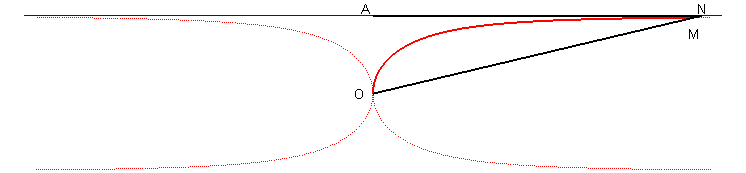The Kappa is the radial curve of the tractrix as well as a special case of nodal curve.

See the construction of the right strophoid from the Kappa.

Do not mistake the Kappa with the bullet-nose curve.

More generally, we can consider the movement of a plane over a fixed plane said of the Kappa, the moving plane being the plane linked to the set square above (the Kappa then being the roulette of the vertex of the set square).

With the notations of this page, we have: .
The base is therefore the Kampyle of Eudoxus with polar equation , the rolling curve the parabola , and the roulettes the curves: : in the movement of the Kappa, there is an exchange of the base and the rolling curve with respect to the conchoidal movement.

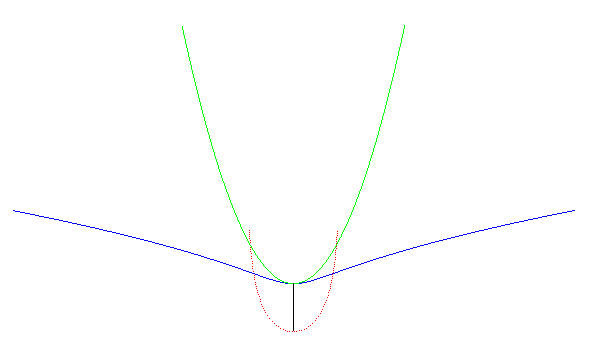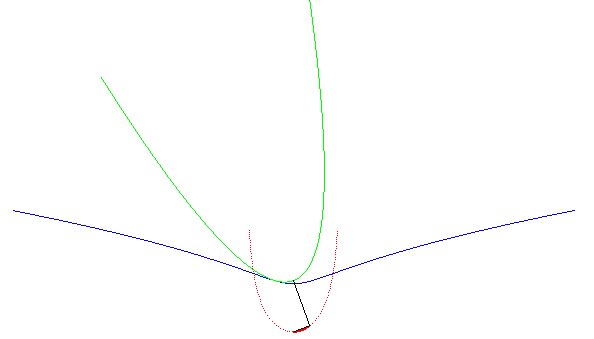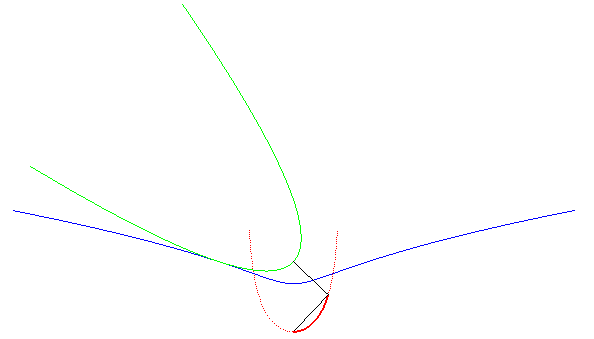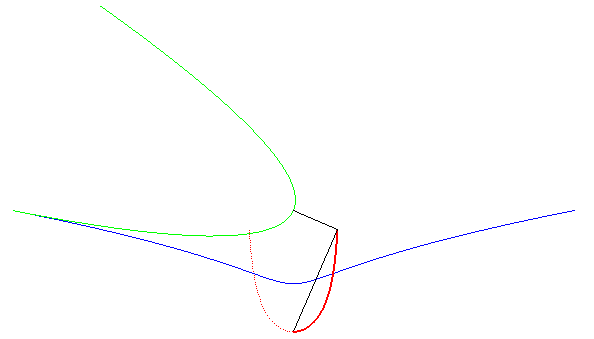The Kappa is a roulette of the movement associated to a parabola rolling on a Kampyle.

next curve previous curve 2D curves 3D curves surfaces fractals polyhedra