Notion studied by Tucker in 1864.

 

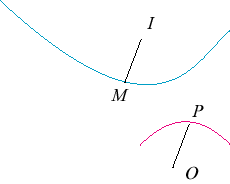
The radial curve of a curve , associated to a fixed point O, is the locus of the points P defined by  where  is the vector joining the current point on  to its centre of curvature; in other words, it is the locus of the end of the radius-of-curvature vector, attached to a fixed point.

 

For an initial curve  with current point , the radial curve is the set of points . Cartesian parametrization of the radial curve: . Complex parametrization: . If the intrinsic equation 2 of the initial curve is , then the polar equation of its radial curve is .

The radial curve of an algebraic curve is an algebraic curve of the same degree as its evolute.

Examples:
 

initial curve	associated radial curve
circle	circle
ellipse	sextic  with equation i.e.  (Loria p. 308)
parabola	duplicatrix cubic
cycloid (with rolling circle with radius R)	circle with radius 2R
deltoid	regular trifolium
astroid	quatrefoil
epicycloid with parameter q	rose
hypocycloid with parameter q	rose
catenary of equal strength	line
catenary	kampyle of Eudoxus
tractrix	kappa
involute of a circle	Archimedean spiral
clothoid	lituus
logarithmic spiral	logarithmic spiral
Ribaucourt curve of index k the cases k = -2, -1, and 2 amount to the above cases of the parabola, the catenary and the cycloid.	Clairaut's curve of index k-1
pseudo-spiral of index n the cases n = 0 , 1, and -1/2 amount to the above cases of the circle, the clothoid and the involute of a circle.	Archimedean spiral of index

See an application of radial curves for wheel-road couples.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017