Curve studied by Puiseux in 1844 and by Pirondini in 1892 and 1905, after whom it is named. Geminiano Pirondini 1857 - 1914: Italian mathematician.

 
 

Intrinsic equation 1:  with n real number different from -1. Intrinsic equation 2: . Cartesian parametrization: . Curvilinear abscissa: s = at. Radius of curvature: .

The pseudospiral (of Pirondini) of index n is the curve the curvature of which is proportional to the n-th power of the curvilinear abscissa. It is a generalisation of the clothoid (case n = 1), that also includes the cases of the circle (n = 0), of the logarithmic spiral (n = -1), of the involute of a circle (n = -1/2), and of a limit case of alysoid (n = -2).

It assumes, for t > 0, the following shapes:
 

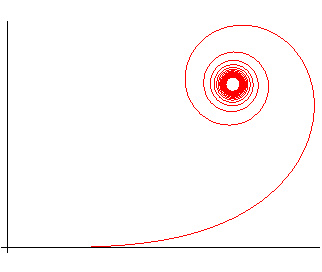
n > 0

-1 < n < 0

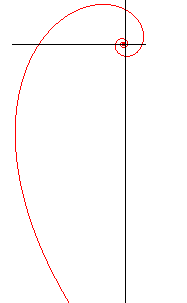
n < -1

An important property, that explains the case of the involute of a circle, is that the evolute of the pseudospiral of index n is a pseudospiral of index  (intrinsic equation ).
The radial of the pseudo-spiral of index n is the Archimedean spiral of index , .

Its Mannheim curve is the curve with Cartesian equation: .
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017