RIBAUCOUR CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
RIBAUCOUR CURVE

| Problem posed by Jean Bernoulli in 1716, solved by Taylor
in 1717; curve then studied by Ossian Bonnet in 1844 and Ribaucour in 1880.
Albert Ribaucour (1845-1893): French mathematician and engineer. See also this link. |
| Second order differential equation: First order equation: Cartesian equation: 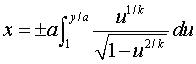 . .
Cartesian parametrization: Algebraic curve for k odd integer. Curvilinear abscissa given by Radius of curvature: |
|
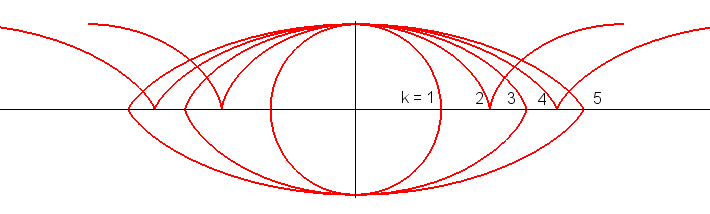
For k a positive integer, we can take any value of t; the curve is closed when k is odd, periodic when k is even. |
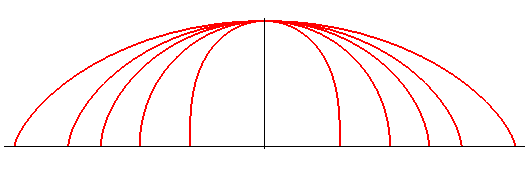 |
When k is positive and not an integer, take |
Case k = -1/4, -1/2, -1 (catenary), -2 (parabola). |
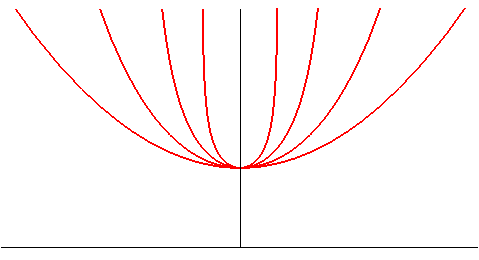
When k negative, take |
| A Ribaucour curve is a curve for which any point M
on the curve satisfies |
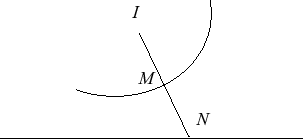 |
In other words, with Ox as the line (D), they are the curves such that the radius of curvature is proportional to the normal: Rc = – k N.
The Ribaucour curve of index k is also the locus
of the pole of the sinusoidal
spiral:
rolling without slipping on (D), with
.
Finally, it is the solution to the calculus of variations
problem that consists in determining the curve for which the integral
is extremal; this is why it is also the trajectory of a light ray in an
inhomogeneous medium: see this
page devoted to the Fermat principle.
Special case:
| Index of the Ribaucour curve | Nature of this curve | Index
of the rolling sinusoidal spiral |
Nature of this spiral | figure | Integral for which the Ribaucour curve is an extremum | Interpretation |
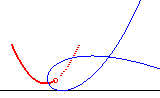
| k = –2 | parabola with directrix (D) | n = –1/3 | Tschirnhausen cubic, with tracing point at the focus |
 |
||
| k = –1 | catenary with base (D) | n = –1/2 | parabola, with tracing point at the focus |
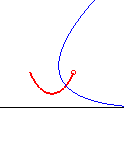 |
curve joining A to B for which the area of the surface spanned by its rotation around (D) is minimal, such a surface is a catenoid. | |
| k = –1/2 | see the last column | n = –2/3 | central negative pedal of the rectangular hyperbola |
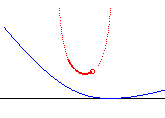 |
homogeneous massive wire joining A to B with minimal moment of inertia | |
| k = 0 | point | n = –1 | line | .... | .... | |
| k = 1/2 | rectangular Sturm roulette
or right lintearia |
n = –2 | rectangular hyperbola |
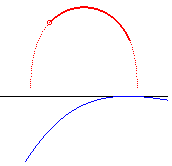 |
? | |
| k = 1 | circle centred on (D) | n infinite | .... | geodesic in the Poincaré half-plane | ||
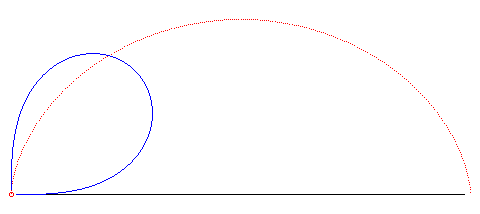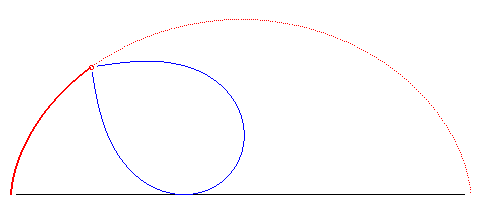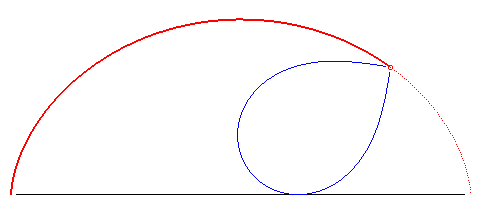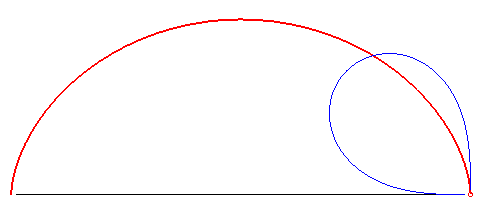
| k = 3/2 | n = 2 | lemniscate of Bernoulli | see the animation above | ? | ||
| k = 2 | cycloid with cuspidal points on (D) | n = 1 | circle, with tracing point on the circle | 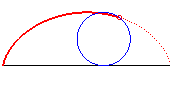 |
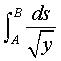 |
brachistochrone curve |
| k = 3 | sextic
|
n = 1/2 | cardioid, with tracing point at the tip | 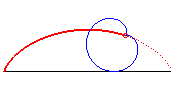 |
? | |
| k infinite | line | n = 0 | point | the line is the shortest path from a point to another... |
Nota: the equation
shows that the Ribaucour curves, for k different from 0, can be
defined by
;
we can then consider that the curve of order 0 is the curve defined by
which is none other than the catenary
of equal strength.
Derivation of the equations from the 3 definitions above:
| Proof starting with the definition by the property of the normals. | Proof starting with the rolling sinusoidal spiral | Proof starting with the calculus of variations problem |
| The equation Rc = - k N can
be written |
The equation of the roulette of the pole of the curve
with polar equation |
The Euler-Lagrange equation applied to the integral |
The Mannheim curve
of a Ribaucour curve is a Ribaucour curve with parameter k – 1.
The rotation of a Ribaucour curve around the Ox
axis gives a rotation
surface whose principal curvatures are
proportional
at each point.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017