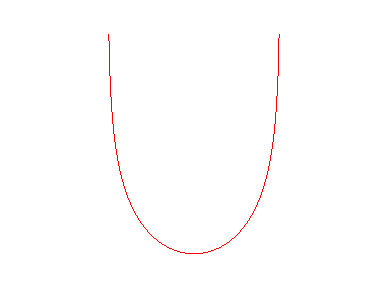
CATENARY OF EQUAL STRENGTH
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CATENARY OF EQUAL STRENGTH

| Curve studied by Finck
and Bobillier in 1826 and Coriolis
in 1836.
Other names: Coriolis' catenary, longitudinal curve, curve of the log cosine. |
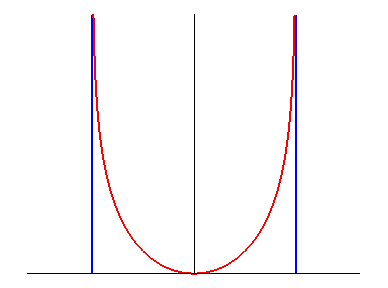
The catenary of equal strength differs from the classic catenary in its two asymptotes. |
Differential equation: Cartesian equation: Curvilinear abscissa: Cartesian tangential angle: Radius of curvature: Intrinsic equation 1: Intrinsic equation 2: Area delimited by the curve, Ox, and the asymptotes: Transcendental curve. |
The catenary of equal strength is the shape taken by an
inextensible flexible massive wire hanging from two points, when the linear
mass density (i.e., in practical terms, the width of the wire) is proportional
to the tension.
Such a wire is not more likely to break in any point
than in another.
This curve, upside-down, represents the profile of a vault without
overload (Brocard) ??
| With the notations of the opposite figure ( This simplifies to |
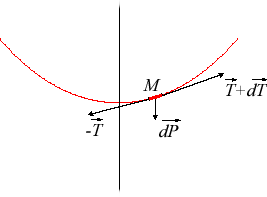 |
The linear mass density is then equal to ,
which sets the width of such a wire.
The formula
shows that the projection of the segment radius of curvature on the x
axis has constant length; this property is a characteristic of the catenary
of equal strength.
| The catenary of equal strength is also the special case
k
= 1 of the family of curves with intrinsic equation 1 Opposite, an animation for k ranging from 0 to 6, with stops at k =1 (catenary of equal strength), k = 2 (syntractrix), and k = 4. |
 |
See also Ribaucour curve, of which the catenary of equal strength can be considered to be a special case.
The radial curve
of the catenary of equal strength is the line x = a and its
Mannheim
curve is a catenary.
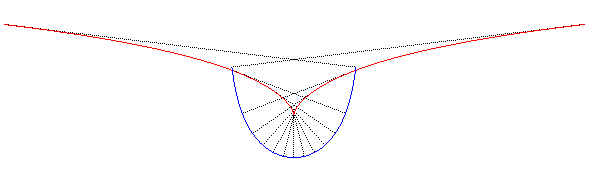
| The evolute
of the catenary of equal strength is the curve with parametrization: |
 |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017