BRACHISTOCHRONE CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
BRACHISTOCHRONE CURVE

| Curve studied and named by Jean Bernoulli in 1718 and
Euler in 1736.
From the Greek brakhisto "the shortest" (therefore written with an "i" and not a "y") and chronos "time". See also mathshistory.st-andrews.ac.uk/HistTopics/Brachistochrone/ |
| Functional equation: Differential equation (obtained by
applying the Euler-Lagrange
equation): |
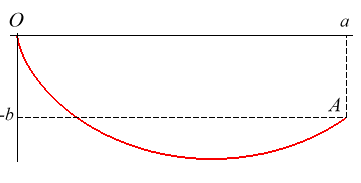 |
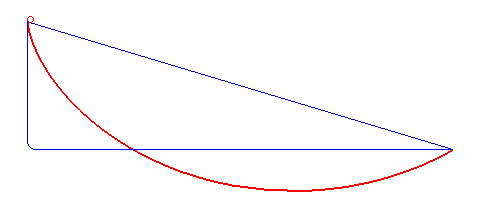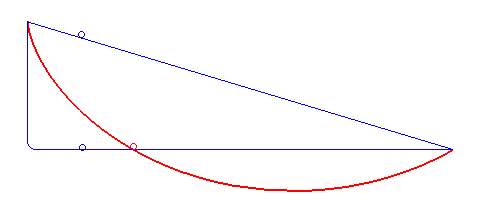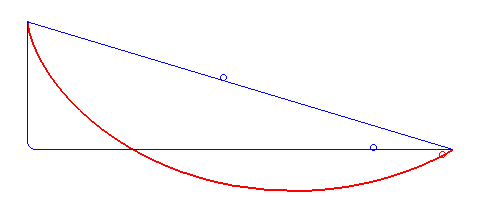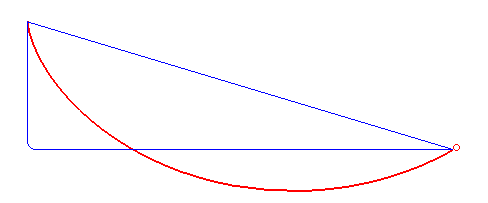
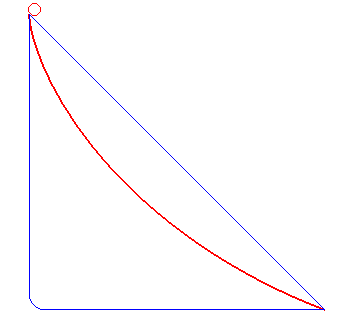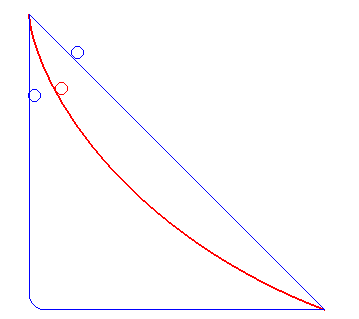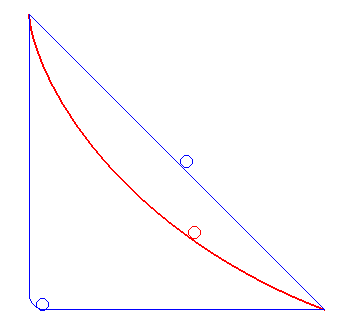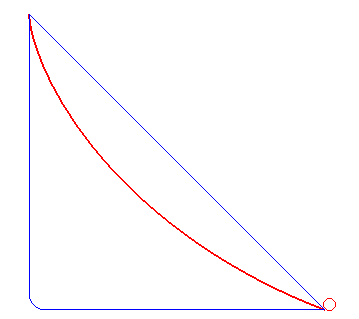
The brachistochrone (curve) is the curve on which a massive point without initial speed must slide without friction in an uniform gravitational field in such manner that the travel time is minimal among all the curves joining two fixed points O and A (here A(a,-b)).
Solution for a > 0 (result found at the same time by Leibniz, Newton, L'Hospital, Jean and Jacques Bernoulli): an arc of a cycloid starting with a vertical tangent.
It can be noted that if the slope b/a between O and A is less than 2/p »63%, corresponding to an angle of »32 ° with the horizontal, the fastest curve has, as in the figure above, a portion that goes upwards!
This is valid in the limit when the points O and A are at the same altitude, in which case the straight line would have an infinite travel time.
|
For - - - - |
 |
| Here the two balls are side by side for a while, then
the blue one follows a straight horizontal line. The cycloid is still the
fastest!
Animation dedicated to editorial board of the TV show "incredible experiments" on France 2 that struggles to accept this phenomenon... |
 |
| The way Jean Bernoulli posed the problem was slightly
different: find the curve minimising the travel time from a point O,
without initial speed, to a vertical plane (at an indefinite point). The
solution is half an arch of a cycloid with a vertical start and horizontal
end, perpendicular to the plane. At the end point, the moving body's altitude
decreased by |
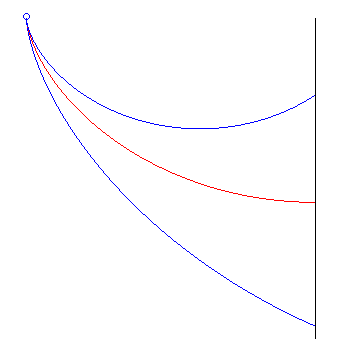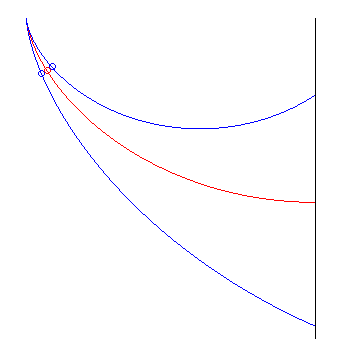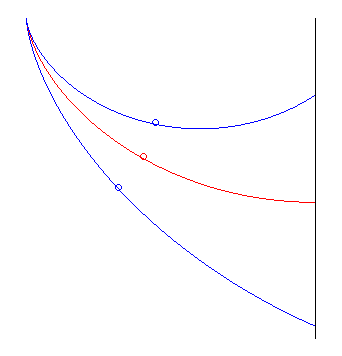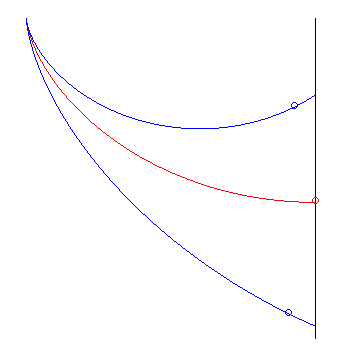
the red cycloid beats the other two |
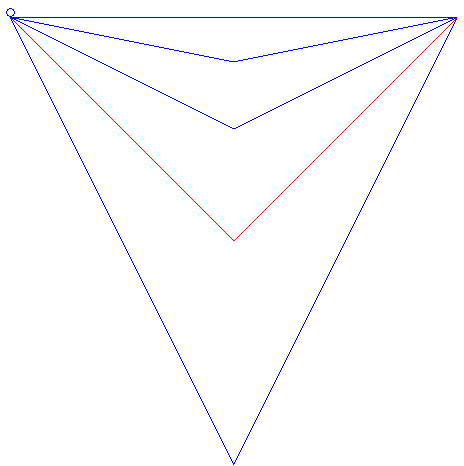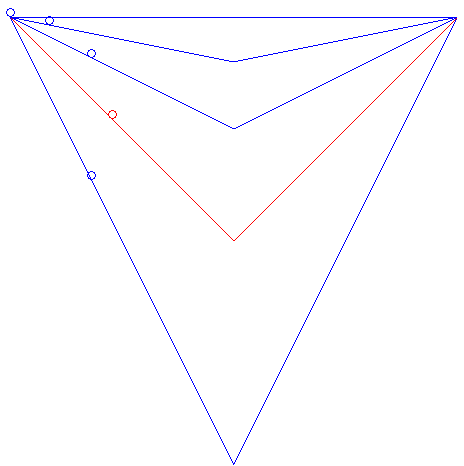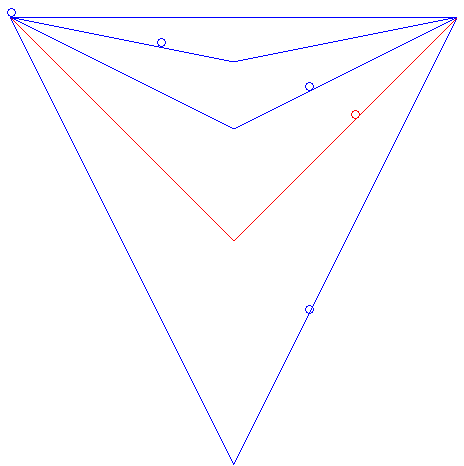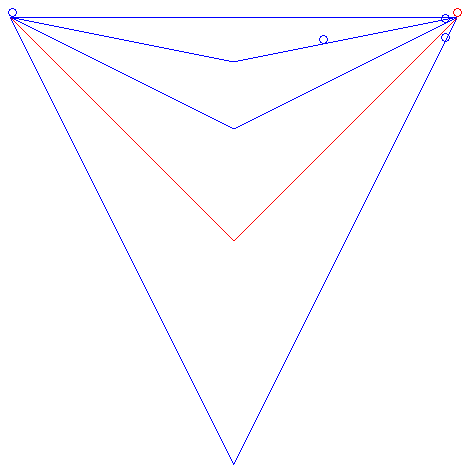
| It can also be asked what the brachistochrone curve among
the curves joining two points and having a given shape would be.
For example, for two points at the same altitude and V-shaped curves, the brachistochrone curve is the one for which the angle of the V is a right angle, as is shown in the animation opposite. This example also shows that among all the linear paths starting at a given point A and ending on a given vertical plane P, the brachistochrone is the one making a 45° angle with the horizontal and that is traced in the vertical plane passing through A and orthogonal to P (result obtained by Galileo in 1638). The problem of the brachistochrone with given length is studied on this page. |
 |
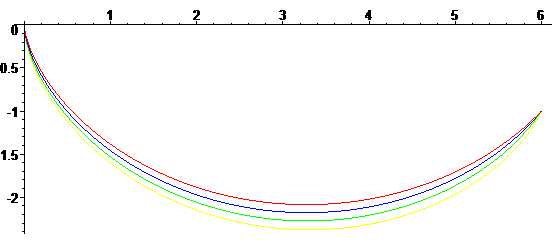
| One can also try to find the brachistochrone "with friction".
We get the parametrization See this article. |
 |
|
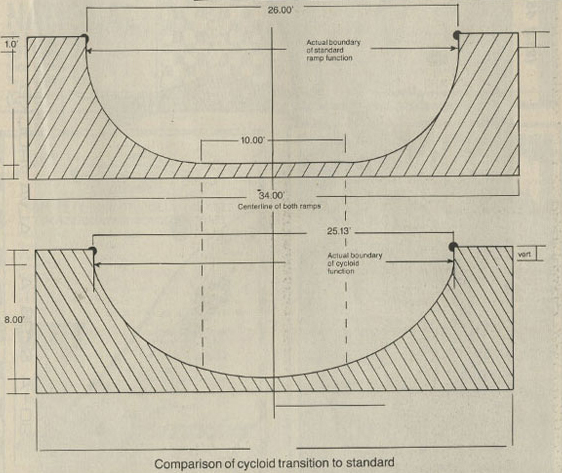
Do the creators of skateboard ramps know that the fastest ramp has the shape of a cycloid? The answer is yes according to the article from which the opposite pictures are taken, but apparently, no cycloidal ramp was ever created. |
 |
We can also look for the brachistochrone curves obtained
for various
speed laws.
Here ,
but for the more general case
,
the differential equation of the brachistochrone is
.
If ,
the brachistochrone we get this time is an arc of a circle.
If now the speed only depends on the distance to O
(), the differential
equation of the brachistochrone is
.
For ,
the brachistochrone is the logarithmic
spiral ; this case corresponds to a moving body in a reference frame
in uniform rotation around O (hence subject to the centrifugal force)
when the speed at O is zero.
| If there is zero speed at distance a to O,
then The case See for example mathworld and this text. |
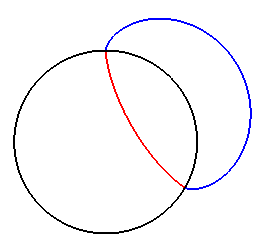
In red, the brachistochrone tunnel. |
For other curves describing the movement of a massive
point in a gravitational field under certain conditions, see isochrone
curve of Huygens, tautochrone
curve,
synchronous curve,
synodal
curve, et L'Hospital
quintic.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017