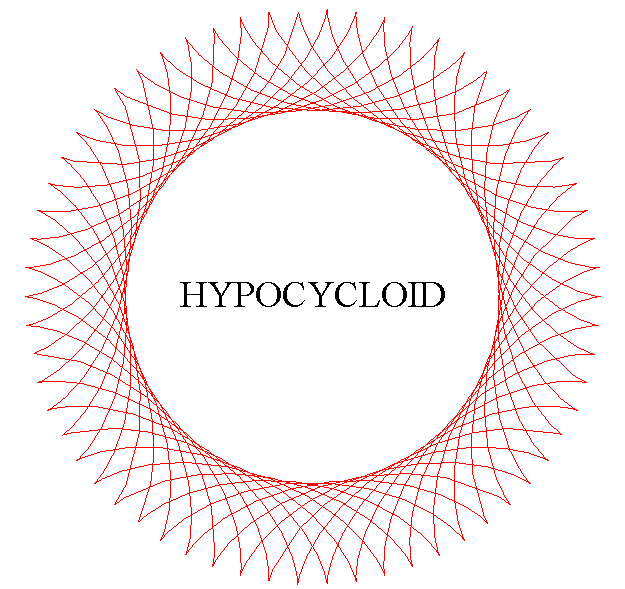
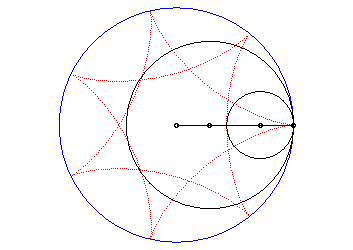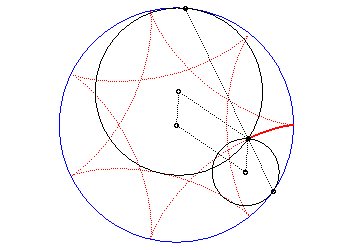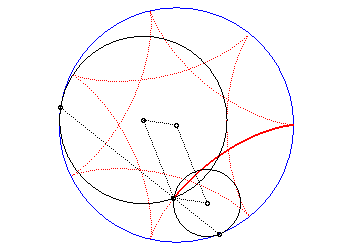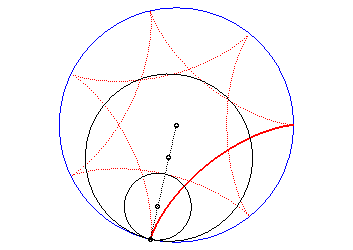
The hypocycloids are the curves described by a point on a circle (C) rolling without slipping on, and inside, a base circle (C₀), when the rolling circle is smaller than the fixed one. Therefore, they are special cases of hypotrochoids.

Complex parametrization:  where a is the radius of the base circle and  that of the rolling circle (q > 1). Cartesian parametrization: . Radius vector: ; polar angle given by . Curvilinear abscissa given by  (hence the differential equation: ).  Two possible expressions for the curvilinear abscissa:  1)  2) . Cartesian tangential angle: 1)  or 2) . Radius of curvature: 1)  or 2)  Intrinsic equation 1 (form 1): . ( is the equation of a hypocycloid if and only if d < c, with ) Intrinsic equation 2 (form 1): . ( is the equation of a hypocycloid if and only if |B| > 1). Pedal equation: . Equation of the tangent at M(t): . Length of an arch: . Area of the surface between the arch and the two tangents at its ends: . When q is an integer, the total length is therefore equal to  times the length of the base circle, and the total area is equal to  times the area of that circle.

The hypocycloids are curves composed of isometric arcs (the arches) connecting at a number of cuspidal points (obtained for ) equal to the numerator of q if it is rational or an infinite number of cusps otherwise.
When q is rational, , the curve is algebraic and rational (take  as a parameter).
It has the same structure as a regular polygon, crossed if m ³ 2, with n vertices linked from m to m by curves located inside the circle (C₀).

The notion of simple hypocycloid with n cusps (E_n) refers to the case q = n, i.e. when there are no crossings.

If we take 0 < q < 1 in the formulas above, then the rolling circle is larger than the base circle; we are therefore in the case of the pericycloids, which also are epicycloids for which the ratio between the base circle and the rolling circle is equal to  (so, if we take  in the formulas above, we get the epicycloid with n cusps).

For q > 1, when b is changed into a – b (i.e. q into  or  into  in the rational case), the curve is not modified. This constitutes the property of double generation of the hypocycloid:

Therefore, we get all the possible hypocycloids by taking only b £ a/2 , i.e. q³ 2:
Note that the hypocycloid with parameter q = a/ b  (irreducible representation of q) has the same shape as the crossed regular polygon with symbol {a/b}
 

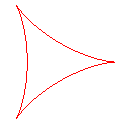
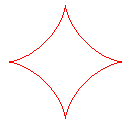
q = 1: point	q  = 2: La Hire line	q = 3: deltoid	q = 4: astroid	q = 5
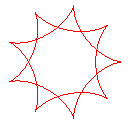
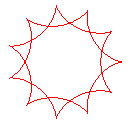
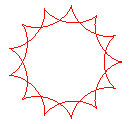
q = 5/2	q = 7/2	q = 9/2	q = 11/2	q = 13/2
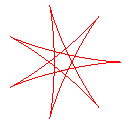
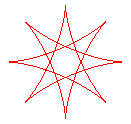
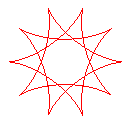
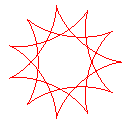
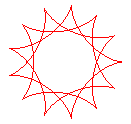
q  = 7/3	q = 8/3	q = 10/3	q = 11/3	q = 13/3
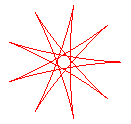
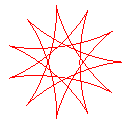
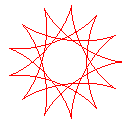
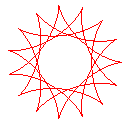
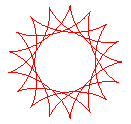
q = 9/4	q = 11/4	q = 13/4	q = 15/4	q = 17/4
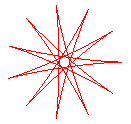
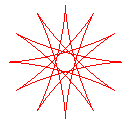
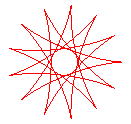
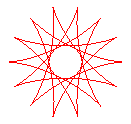
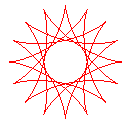
q = 11/5	q = 12/5	q = 13/5	q = 14/5	q = 16/5

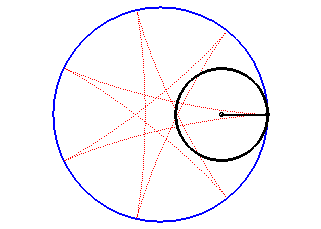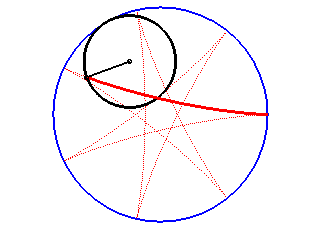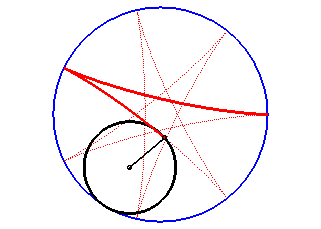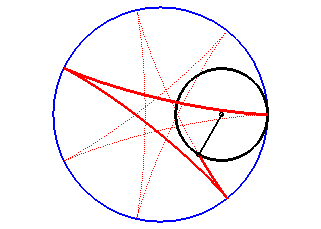
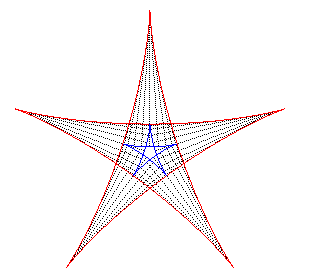
The hypocycloid is the envelope of a diameter of a circle with radius equal to twice that of (C), rolling without slipping on, and outside, (C₀).

It is also the envelope of a chord (PQ) of the circle with centre O and radius  (circle of the vertices of the hypocycloid), when P and Q travel along the circle in opposite directions with speeds forming the constant ratio q – 1 (this constitutes the Cremona generation).
Finally, it is the negative pedal with respect to O of the rose: .
Its evolute is its own image by the direct similarity with centre O, ratio , and angle .

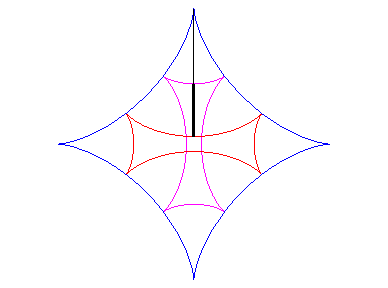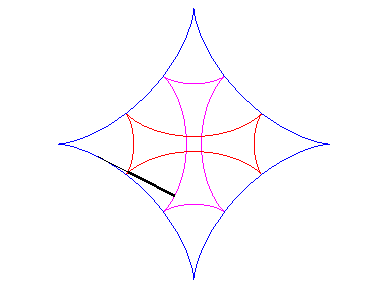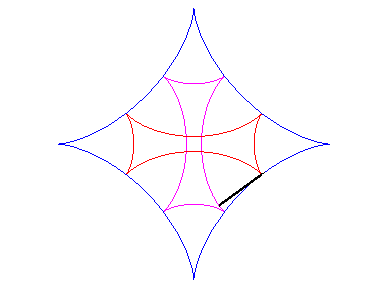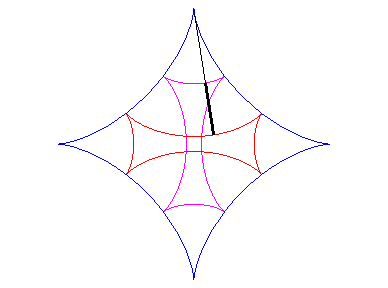
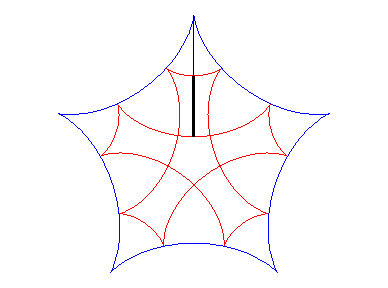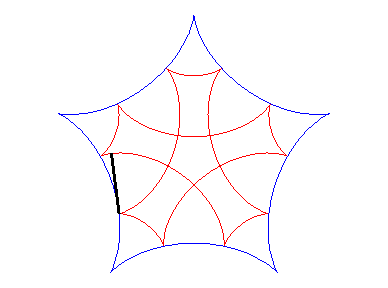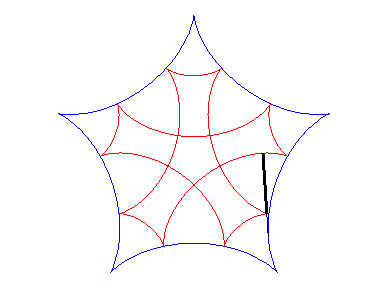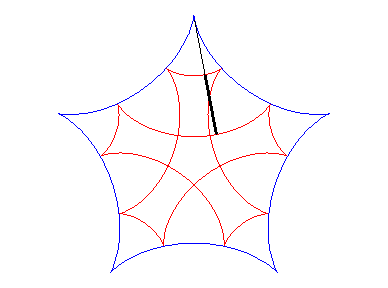
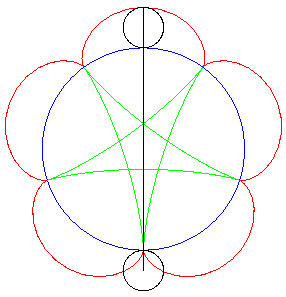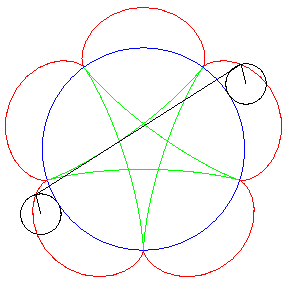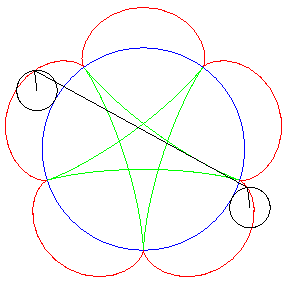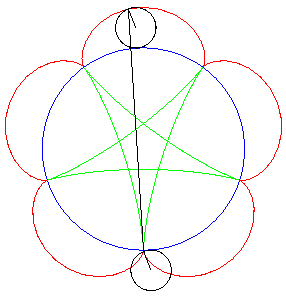
If two tracing circles, symmetric images of one another about the centre of the fixed circle, roll inside the base circle in phase opposition, then the segment line joining these two points (which has constant length) envelopes another hypocycloid, with parameter ; opposite, the cases q = 4 and 5 ; when q = 3, q' = 3 (see the remarkable construction and its application at deltoid).
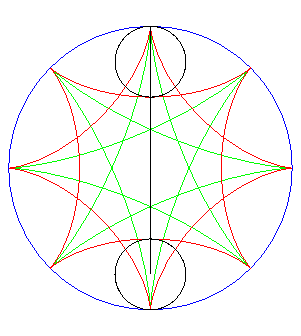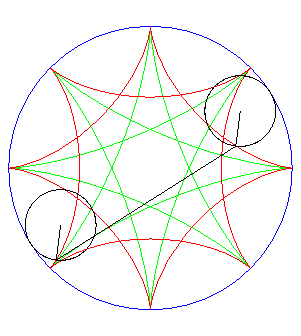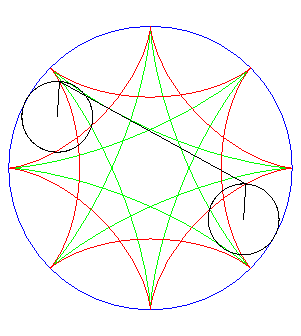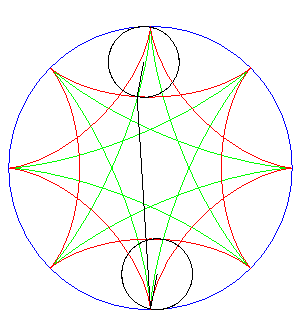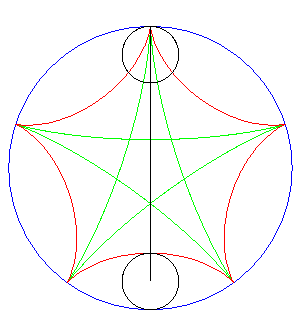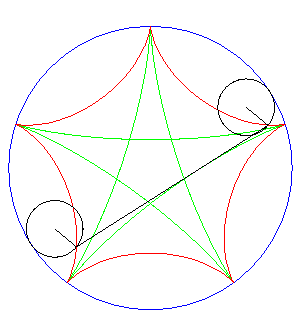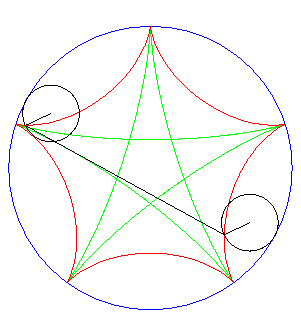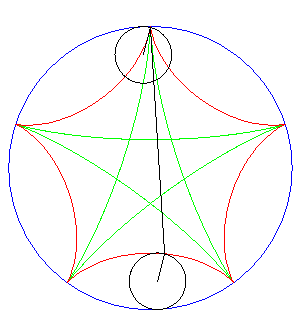Ditto if the tracing circles are outside the fixed circles; when the points P et Q trace an epicycloid with parameter q, the segment line PQ envelopes again a hypocycloid with parameter ; opposite, the cases q = 4 and 5; when q = 3, q' = 3 (see at deltoid).

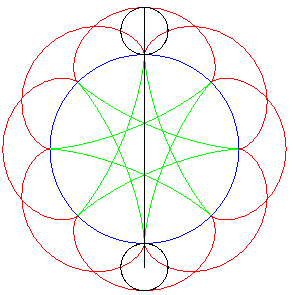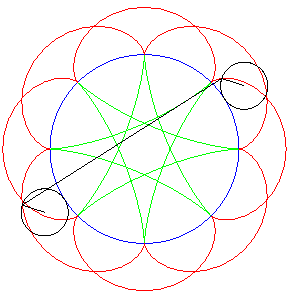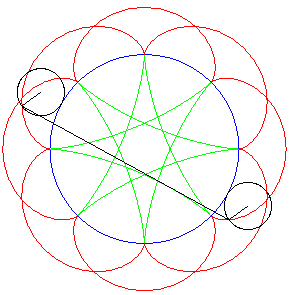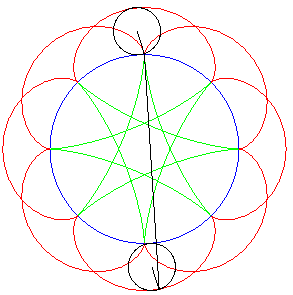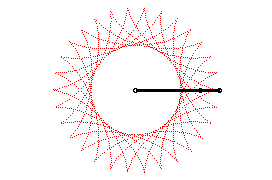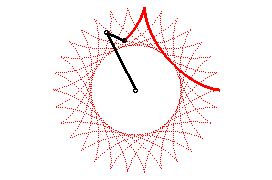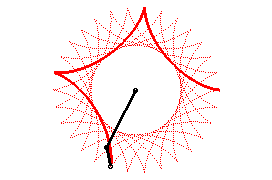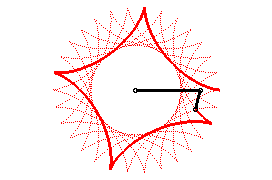
The hypocycloids can also be defined as the trajectories of a motion that is the sum of two uniform circular motions with same speed and opposite directions (with complex parametrization:  with ).

The hypocycloids are also projections of spherical helices, and, finally, the curves of small oscillations of the Foucault pendulum.

The differential equation  proves, thanks to the Euler-Lagrange equation, that, as the cycloid, the hypocycloid is a brachistochrone curve: it is the plane curve that minimises the travel time of a moving point subject to a central force field proportional to 1/r and moving freely along this curve; it is therefore the shape of a tunnel dug in the Earth that would minimise the travel time from a point A to a point B on the surface, by the pull of gravity.

See also, in 3D, the spherical cycloids.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017