Property of the cycloid discovered by Huygens in 1673.

The isochronous curve of Huygens is the curve such that a massive point travelling along it without friction has a periodic motion the period of which is independent from the initial position; the solution is an arch of a cycloid the cuspidal points of which are oriented towards the top; the fact that it is isochronous comes from the fact that it is tautochronous. The period of the movement is  where L is the sagitta of the cycloid.

The cycloidal pendulum of Huygens below uses this property and the fact that the evolute of a cycloid is an equal cycloid. It is interesting because of its oscillation period of T = , independent from the amplitude, as opposed to the free pendulum only the "small" oscillations of which can be considered as having the period T.

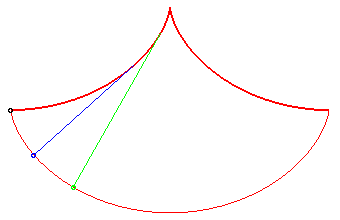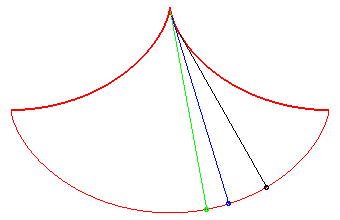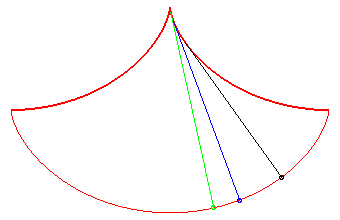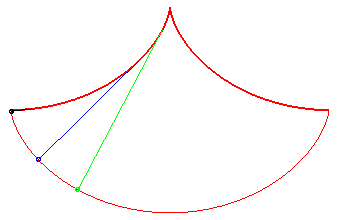
In this problem posed by Huygens, all the points reach the bottommost point at the same time; Galileo posed the same problem, but for massive points moving on linear stands: see synchronous curve.
 

See also the isochronous curve of Leibniz and the isochronous curve of Varignon for another type of isochronous property, and at synodal curve, brachistochrone curve and tautochronous curve.
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017