Curve studied by Cotes and Maclaurin in 1722. Lituus (Latin word): wand used by Roman augurs, similar to a current bishop's staff.  Other name: limaçon spiral.

 
 

Polar equation: . Curvilinear abscissa: . Radius of curvature: . Transcendental curve.

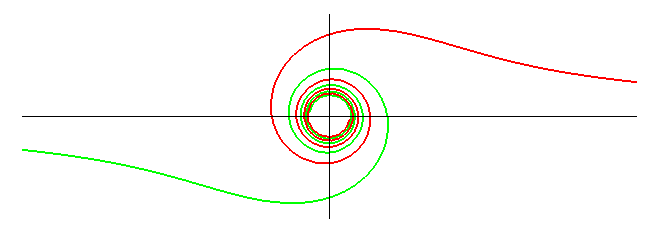The lituus is the locus of the point M on a variable circle centred on O cutting the axis Ox at A such that the area of the circular domain OAM is a constant equal to a²/2.

The inflexion point is obtained for q = 0,5 radians, i.e. around 30°.

The lituus is the inverse with centre O of the Fermat spiral and the radial of the clothoid.

It can be found in the volutes of Ionic capitals:

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL  2017