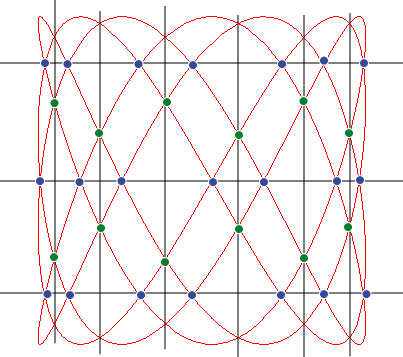
Those who see this movement in the red figure are, supposedly, "right-brain", those who see the oppose movement are "left-brain"....

Why can't we see this movement in the red figure?

Reduced Cartesian parametrization:  ().

The Lissajous curves are the trajectories of a point the components of which have a sinusoidal movement.

The Lissajous curves of parameter n (ratio between the frequencies of the two sinusoidal movements) are the projections on the planes passing by the axis of the cylindric sine waves of parameter n:
as well as of the cylindric sine waves of parameter 1/n: .
The curve whose reduced parametrization is in the header is indeed the projection on xOy of the cylindric sine wave of axis Oy and parameter n and the projection on xOy of the cylindric sine wave of axis Ox and parameter 1/n .
 

If n is irrational, then the curve is dense in the rectangle .
 

If n is a rational number whose irreducible form is , then it is more convenient to use the following equations:

Cartesian parametrization:  ,  . Algebraic curve of degree 2q if  when p is odd and  when p is even. Portion of an algebraic curve of degree q if  when p is odd, or if  when p is even. The number of double points is, in general, equal to  (p–1 groups of q points aligned on lines parallel to Ox, in blue opposite, and q–1 groups of p points aligned on lines parallel to Oy, in green opposite). In the case where the curve can be described in both directions, then there are  double points.

We get a portion of the plot of the n-th Chebyshev polynomial T_n when n is an even integer, and when n is an odd integer,  .
Here are some special cases, with a = b:
 

When n = 1, we get the ellipses:
 

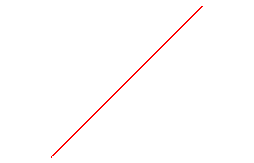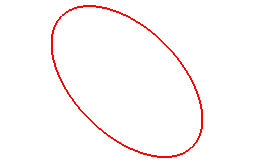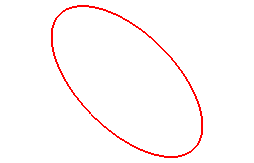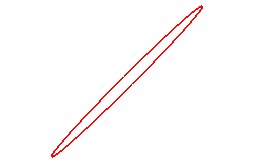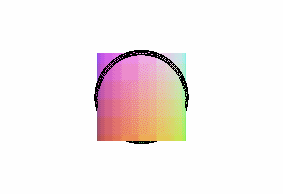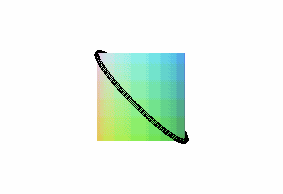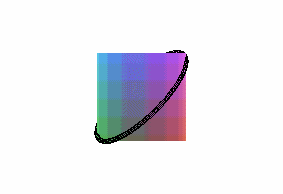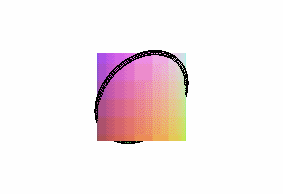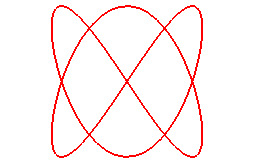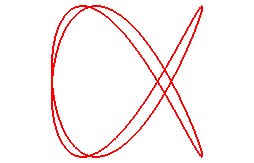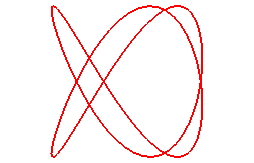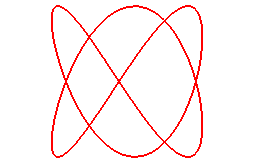
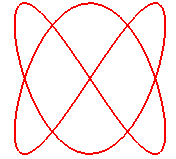
When n = 2 (q = 2, p = 1), we get the besaces:
 

: lemniscate of Gerono

: portion of a parabola.

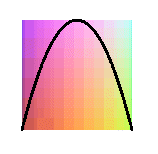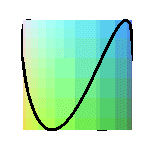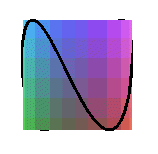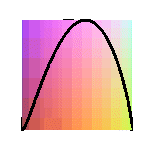
projections of the cylindric sine wave of parameter 2 ( pancake curve)

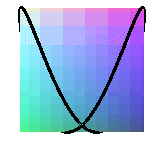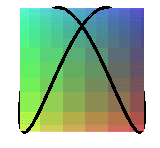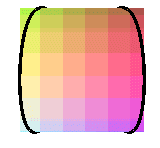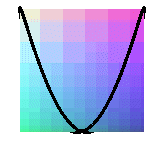
projections of the cylindric sine wave of parameter 1/2 ( Viviani's window)

When n = 3/2 (q = 3, p = 2):

:  Sextic with Cartesian equation

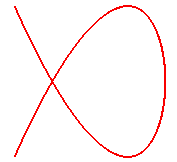Portion of the divergent parabola with equation:.

cylindric sine wave of parameter 3/2

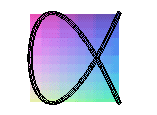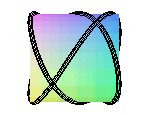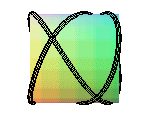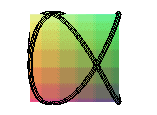
cylindric sine wave of parameter 2/3

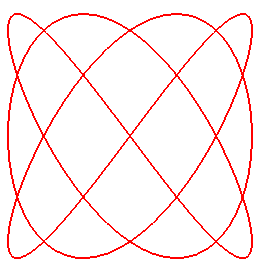Cartesian parametrization (curve on the right):  or  () Cartesian equation:  Polynomialquartic. See here a tied version of it.

n = 5/3

n  = 5/4

n  = 6/5

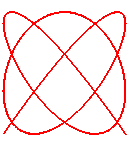n  = 8/5

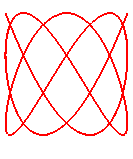n  = 9/8

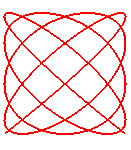The Lissajous curves have the same topology as the curves of billiard balls in a rectangular billiard table. See this page.

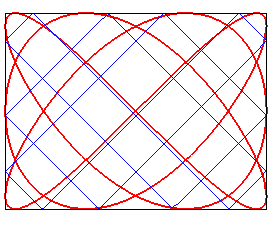One can also imagine "Lissajous curves in polar coordinates", with polar parametrization:  ; opposite the case p = 3, q = 7,  (idea of Ch. de Rivière).

This beautiful doormat does not follow exactly a Lissajous curve. Yet, if in the Lissajous curve , you follow the blue "bridges" opposite, you get this doormat. See an interpretation on this page.

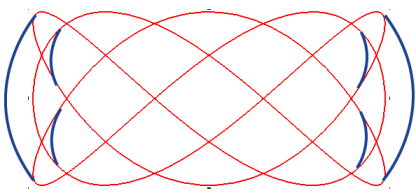See also the 3D Lissajous curves, and the basins.
 
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL 2017