LISSAJOUS KNOT, 3D BILLIARD KNOT
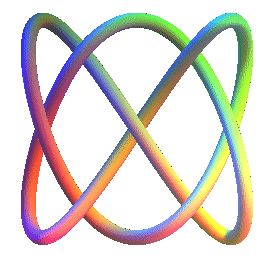
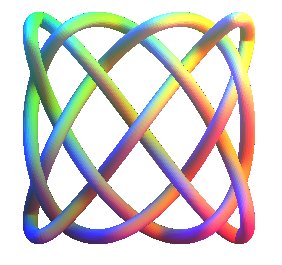
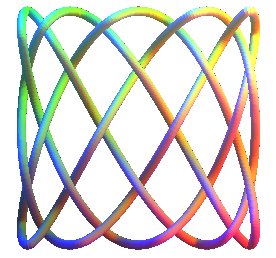
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
LISSAJOUS KNOT, 3D BILLIARD KNOT
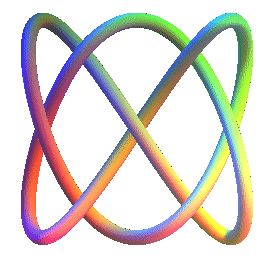
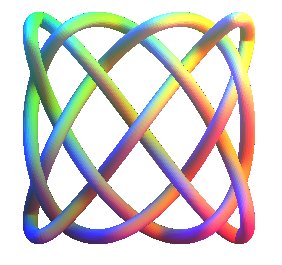
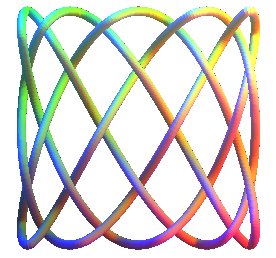
| Knot studied by Bogle,
Hearst, Jones and Stoilov in 1993, Jones
and Przytycki in 1998, Koseleff
and Pecker in 2011.
Wikipedia page. |
| Cartesian parametrization: |
The Lissajous knots are the knots associated to the 3D Lissajous curves when they are closed and without double point.
As is proved in the above article by Jones and Przytycki, they also are the knots associated to the trajectories of a ball (not subject to gravity) in a parallelepipedic billiard, or even a cubic one (imagine a glass box).
It can be proved that for all values of p, q, r, there exist values of j and y such that the knot is trivial, and that certain knots such as the trefoil knot are not Lissajous knots.
When p and q are coprime,
and
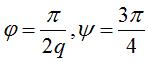
For example, the 3 Lissajous knots represented above are
parametrized by: ,
and
.
The first one is the 4th
prime knot with 7 crossings, written 74,
and more generally, the curve
is, when n is not a multiple of 3, a knot with 5n – 3 crossings
with above/below alternate passages.
It is similar for the curve
for odd values of n, which is a knot with 3n – 2 crossings.
On this
page can be found a list of remarkable Lissajous knots; the canonical
parametrization used in this list is .
| Here is a beautiful case of an open knot: By connecting the ends, we get a trefoil knot. |
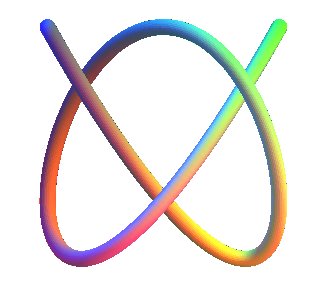 |
We can also generalize to a 3D billiard with a convex polyhedral shape. This way, we get all the possible knots, even if we only consider the billiards with a right regular prism shape (Koseleff and Pecker).

Lissajous knot, abbey of S. Maria di Moie, Italy
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL
2018