3D LISSAJOUS CURVE
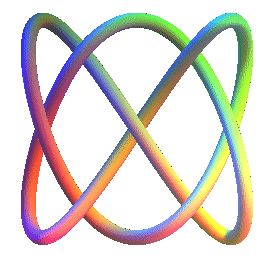
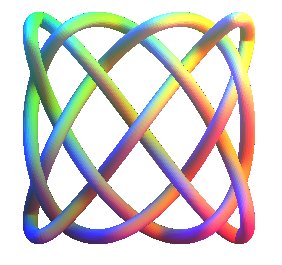
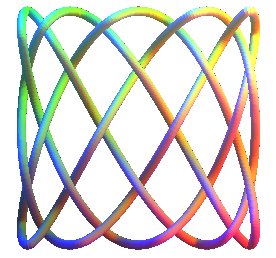
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
3D LISSAJOUS CURVE
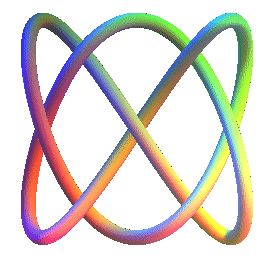
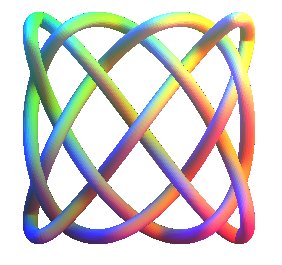
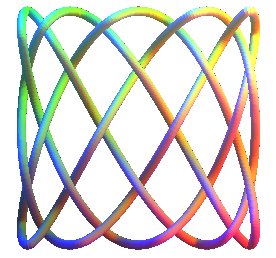
| Curve studied by Bogle, Hearst, Jones et Stoilov in 1993. |
| Cartesian parametrization: |
The 3D Lissajous curves are the trajectories of a point in space the rectangular components of which have a sinusoidal motion.
The projections on the 3 coordinate planes are the classic 2D Lissajous curves.
For n = 1 or n = m, we get a cylindrical sine wave.
We get a closed curve if and only if n and m are rational.
When the curve does not have double points, nor a cusp, it forms a knot in space, called Lissajous knot, equivalent to a cubic billiard knot.
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018