Cartesian parametrization:  n > 0. Cylindrical equation: ; in the following, we take a = b. Curvilinear abscissa: . Radius of curvature: , radius of torsion: .

The cylindrical sine waves are the coiling of a sinusoid around a cylinder (in other words, if we make a cylindrical sine wave roll on a plane, we get a sinusoid).

They are special cases of 3D Lissajous curves.
The projections on the planes containing Oz are the planar Lissajous curves, with parameter n if n > 1, 1/n otherwise.

For n = 1, we get an ellipse, for n = 1/2, Viviani's curve and for n = 2, the pancake curve.

For integral values of n, the number of arches is equal to n. The curve with three arches is used to represent the Borromean rings.
 

When we apply a horizontal projection onto the sphere with center O and radius a, the cylindrical sine wave  becomes the clelia: .

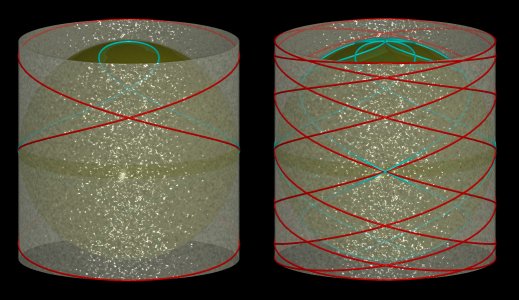
Figure made by Alain Esculier

See also the spherical sinusoids, the 3D basins, the cylindrical tangent waves and the sine tori.
 
 

next curve

previous curve

2D curves

3D curves

surfaces

fractals

polyhedra

© Robert FERRÉOL, Jacques MANDONNET 2018