VIVIANI CURVE
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
VIVIANI CURVE
| Curve studied by Roberval and Viviani in 1692.
Vincenzo Viviani (1622-1703): Italian mathematician. Initial name given by Roberval: cyclo-cylindrical curve. See also the mathourist's page. |
System of Cartesian equations:  .
System of spherical equations: 
(longitude = latitude).
Cartesian equation: 
(where  )
or: 
(with  ),
form used in what follows.
Rational biquadratic
(quartic of the first kind).
|
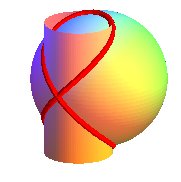
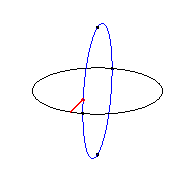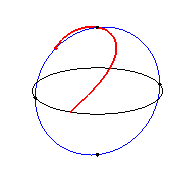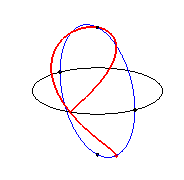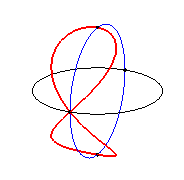
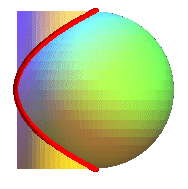
The Viviani curve is the intersection between a sphere
with radius R (here, 
)
and a cylinder of revolution with diameter R a generatrix of which
passes by the center of the sphere (here, 
);
it is therefore a special case of hippopede,
a curve that is at the same time spherical
and cylindrical, as well as
a special case of conical
rose.
Therefore, we get a Viviani curve by sticking the tip of a compass inside a cylinder of revolution and tracing on this cylinder a "circle" with radius equal to the diameter of the cylinder.
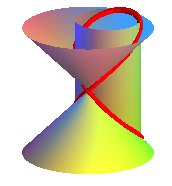
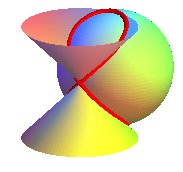
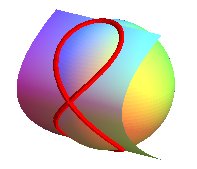
The Viviani curve is also included in a cone of revolution
the axis of which is a generatrix of the above cylinder (here, 
),
as well as in a parabolic cylinder (here, 
),
which gives a total of 6 definitions of the Viviani curve as the intersection
of 2 quadrics, and 3 definitions by the motion of a compass on a cylinder
of revolution, a cone of revolution or a parabolic cylinder.
 |
 |
 |
 |
 |
 |
| By the way, the linear combinations of two of these quadrics gives a infinite family of quadrics that contain the Viviani curve, all of revolution except the parabolic cylinder. |  |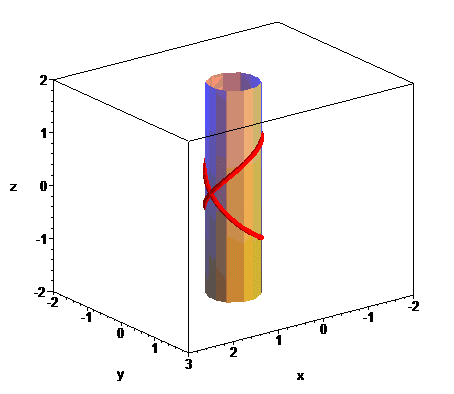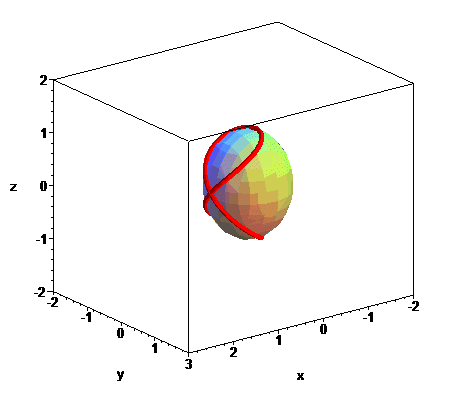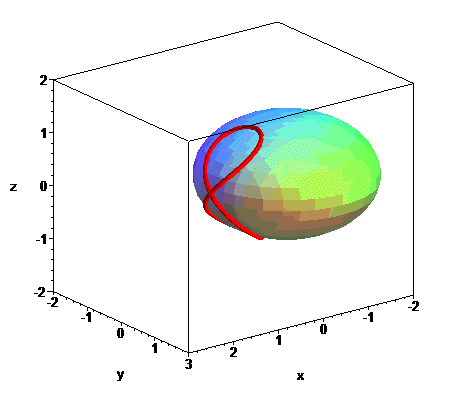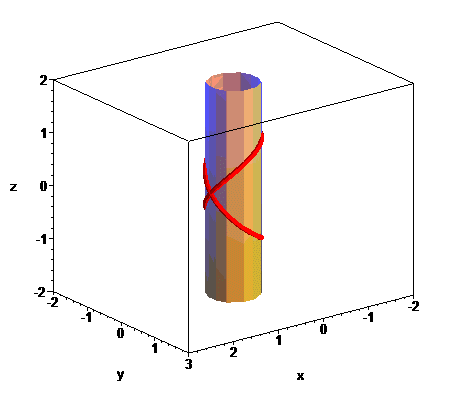
 |
The Viviani curve is also a portion of the section of the Möbius surface by a sphere (section that also includes a great circle of the sphere). |
| The system of spherical equations shows that the Viviani
curve is a special case of clelia.
Therefore, it is also the locus of a point M on a meridian of a sphere turning at constant speed around the polar axis, while the point M moves at the same speed along this meridian. |
 |
| The system of cylindrical equations shows that the Viviani
curve is also a special case of cylindrical
sine wave.
Therefore, if we develop the cylinder on which the Viviani
curve is traced, we get a period of a sinusoid: |
 |
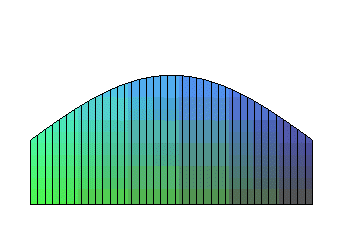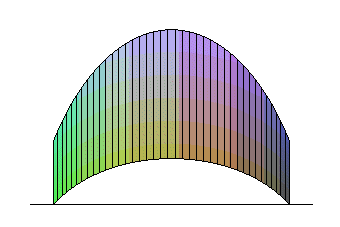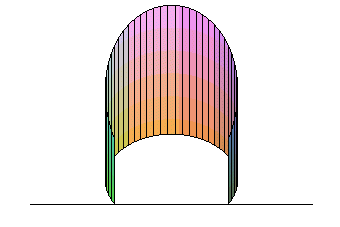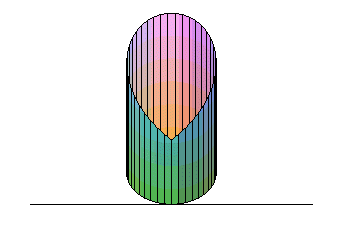
| Opposite, an animation of a sheet delimited by an arch
of sinusoid, that yields a Viviani curve.
Parametrization:  ,
with t between 
and  , u
between 0 and 1, and, in the animation,
ranging from 0,001 to  .
Note that, halfway through (  ),
the curve is a half-ellipse. |
 |
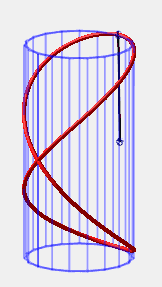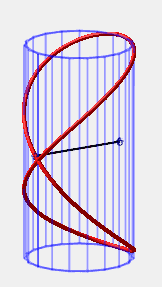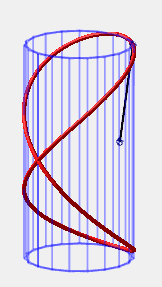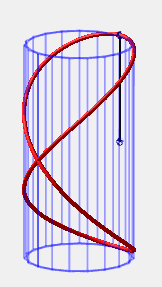
| If one end of a bar of length L is fixed on a
vertical cylinder with diameter L, then the free end, when slipping
along the cylinder because of the gravity, will describe the intersection
between the cylinder and a sphere with radius L centered on it,
in other words, a Viviani curve.
A series of bars identical to the latter generates an elegant animation of hyperboloids of revolution (idea of Andre Hubert).
|
 |
 |
A lot of planar rational quartics are projections of the Viviani curve.
We get:
| a circle on the plane xOy | an arc of parabola on the planes xOy xOz | a lemniscate of Gerono on the plane yOz |
 |
 |
 |
And more generally:
| besaces on the planes passing by Oz | fish curves on the planes passing by Oy | generalized bifoliums on the planes passing by Ox |
 |
 |
 |
The stereographic projection from the North (or South)
pole is the right
strophoid with equation:  . |
 |
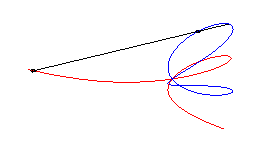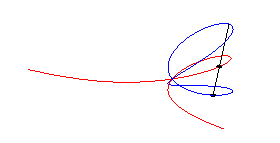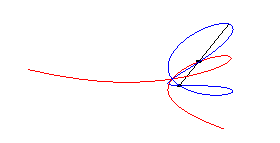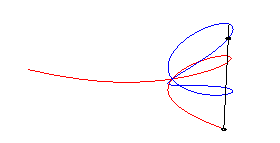| The stereographic projection from the point diametrically opposite the double point is the lemniscate of Bernoulli. |  |
The gnomonic projection (with center O) is a kappa
curve.
 |
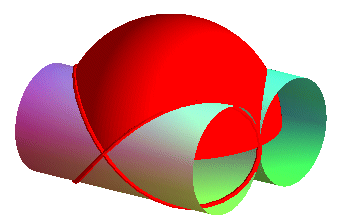As we've seen above, the ratio of the area of the portion
of half sphere located outside the two symmetrical Viviani windows over
R²
is rational, as opposed to the area of the half-sphere; Viviani had called
it: vela quadrabile fiorentina (Florentine veil that can be squared).
Note: I do not know of an example of vela quadrabile fiorentina in architecture.
It had been written that a church in Milan had one, but that was a mistake.
|
See also at surface
of equal slope, the cone
with center O that lies on the Viviani curve, that could be
called "Viviani cone", the surface
obtained by folding a cylindrical sheet of paper along the Viviani
curve.
|
Sphere covered by a lattice of Viviani curves (coordinate lines of the parametrization  ).
See also the cone parametrized by Viviani curves. |
 |
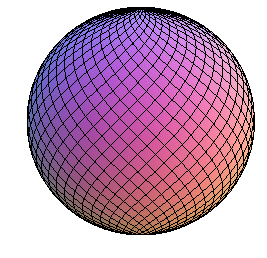Sculptures by Marta Pan in Dallas |
Who will notice the Viviani at the back of this rusted tank? |
| next curve | previous curve | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2018
.
)
where A(a, 0, 0): 
.
and R, written thanks to an elliptic integral, 
.
;
as opposed to that of the circle, the squaring of the complement of this
window on the sphere is possible (area = 8 R²).
;
if we remove two symmetrical Viviani temples from the sphere, the cubing
of the remaining solid (volume 
)
is possible.
,
with 
.
We thus easily obtain a Viviani curve by cutting on a sheet of paper the
figure formed by two arches of sinusoids and glueing the tips.