CONE OF REVOLUTION
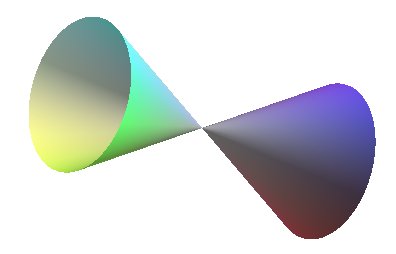
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
CONE OF REVOLUTION
| Writing Cylindrical equation: Cartesian equation: Cartesian parametrization: |
| Another parametrization: |
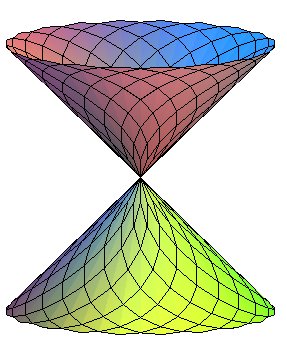 |
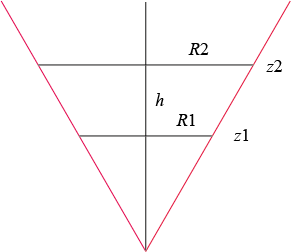
| Volume of the trunc of cone limited by the planes Area : |
 |
The cone can be developed
by mapping a point M of the cone to the point of the plane with
polar coordinates ;
a half-cone will then become an angular domain with angle
.
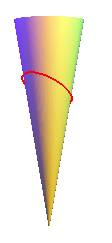
Remarkable curves traced on the cone of revolution:
| - give honor where honor is due: the planar sections
or conics : ellipses, parabolas
and hyperbolas. They can be developped into the polygasteroids
of index n >1.
Cutting by the plane Opposite, the case |
  |
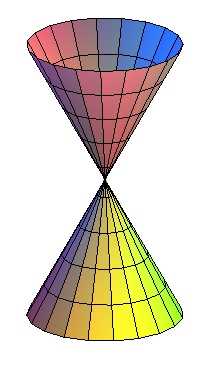
| - the curvature lines, which are the parallels (circles) and the meridians (lines) |
 |
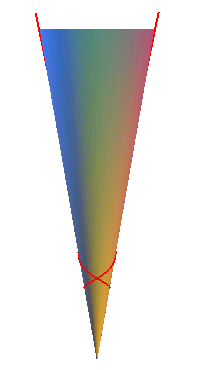
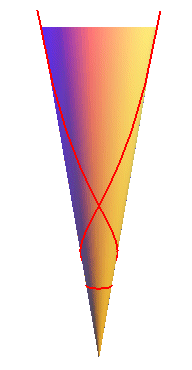
| - the geodesics,
which are the curves that develop into lines; there are the generatrices
and the curves with spherical equation: |
  |
| - the helices, which also are the rhumb lines, which project on xOy as logarithmic spirals: see conical helix. |
|
| - the conical spirals of Pappus, that project on xOy as Archimedean spirals. |
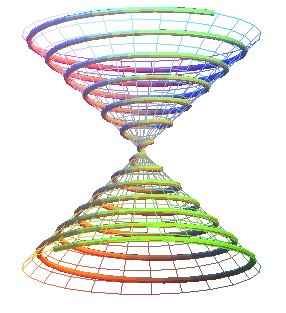 |
| - the hyperbolic conical spirals. |
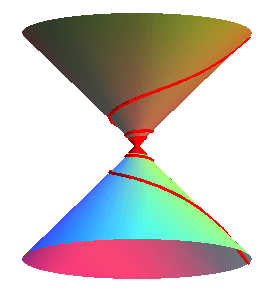 |
| - the conical roses, including Viviani's curve. |
|
| - the conical catenaries. |
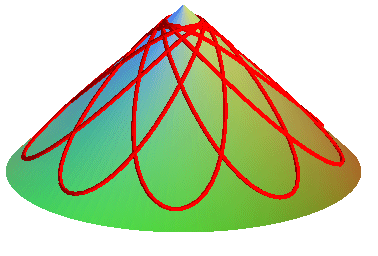 |
See also the spherical cycloids, loci of a point on a cone of revolution rolling without slipping over another cone of revolution, as well as the Cartesian ovals, projections of the intersection between two cones of revolution with parallel axes.
Cones in nature:
 |
 |
 |
and elsewhere:
 |
 |
 |
 |
| next surface | previous surface | 2D curves | 3D curves | surfaces | fractals | polyhedra |
© Robert FERRÉOL 2017