Équation cartésienne générale : , propre (ou éventuellement vide) si la forme homogène associée :  est non dégénérée. Équations cartésienne et polaire dans un repère d’origine un sommet et d’axe des abscisses l’axe focal : , . Équation polaire dans un repère d’origine un foyer et d’axe des abscisses l’axe focal :  ; équation polaire de la directrice correspondante : . Cas des coniques à centre, dans un repère d'origine le centre et d'axe des abscisse l'axe focal : Équation cartésienne : , soit . Équation polaire : .

La définition actuelle d’une conique est d’être une courbe algébrique du deuxième degré.
Cette définition englobe les cas de dégénérescence (dans le plan euclidien : ensemble vide, point, réunion de deux droites) et permet d’affirmer que les coniques sont les sections planes des quadriques.
Cependant, dans ce site, le mot conique désigne uniquement les cas non dégénérés, ou "propres" : ellipse, parabole, hyperbole.

Avec cette acception, voici diverses définitions géométriques des coniques :
     1) Définition des Grecs.
Les coniques sont les sections d’un cône de révolution par un plan ne passant pas par son sommet.
 

Ellipse

Parabole

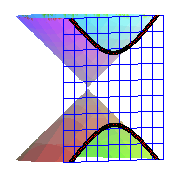
Hyperbole

Le "compas parfait", inventé par un mathématicien perse du Xème, permet de tracer des (portions de) coniques utilisant cette définition. Le bras SM pivote autour de l'axe SO en gardant un angle fixe et donc décrit un cône de révolution d'axe de symétrie SO. Le point M va donc tracer une conique sur la planche. La génératrice rose symétrique de SM par rapport à l'axe coupe manifestement la planche vers la droite, donc la courbe tracée sera une hyperbole. Modèle ci-contre réalisé par Olivia De Cocq et Darwin Libioulle, étudiants à l'Ecole polytechnique de Bruxelles.

    2) Définition par foyer et directrice.

Les coniques sont des cercles, ou les lieux des points dont le rapport des distances à un point fixe (le foyer F) et à une droite fixe (la directrice (D)) est constant (égal à l’excentricité e) ; les ellipses sont obtenues pour e < 1, la parabole pour e = 1, les hyperboles pour e > 1.

Ce n'est qu'en 1822 que Dandelin a relié entre elles ces deux premières définitions, en montrant que les foyers et les directrices sont obtenus à l'aide des deux sphères inscrites :
 

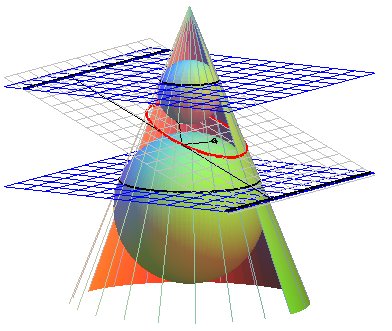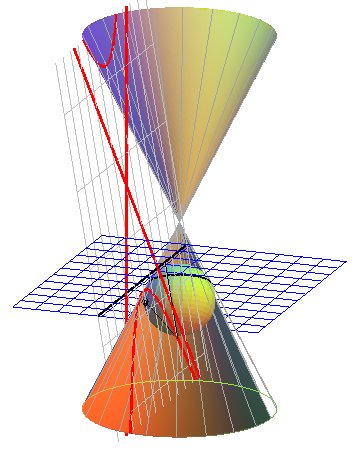    3) Définition par courbe d'équidistance entre un point et un cercle généralisé.
Les coniques sont les lieux des points équidistants d’un point fixe (le foyer) et d’un cercle ou d'une droite (C) (le cercle directeur ou la directrice), c'est à dire les isotèles de cercle généralisé ; autrement dit, ce sont les lieux du centre d’un cercle variable astreint à passer par un point fixe et à être tangent à (C).
Lorsque le foyer est intérieur au cercle, on obtient les ellipses, extérieur les hyperboles, et lorsque (C) est une droite : la parabole.

Plus généralement, les lieux des centres de cercles tangents à deux cercles généralisés de rayons distincts sont des réunions de deux coniques.

    4) Définition par orthocaustique de cercle ou droite.

Les coniques sont les orthocaustiques (ou antipodaires) d’un cercle ou d'une droite (C') (le cercle principal ou la tangente au sommet).

Lorsque la source lumineuse, qui est aussi le foyer de la conique, est intérieure au cercle, on obtient les ellipses, extérieure, les hyperboles, et lorsque (C') est une droite : la parabole.

Les coniques sont donc aussi les enveloppes de la médiatrice d'un segment joignant un point à un cercle ou une droite (le cercle directeur ou la directrice) (autrement dit, ce sont les courbes dont l’orthotomique est un cercle ou une droite).

    5) les coniques sont les anticaustiques de droite.

    La première définition a plusieurs implications dans la vie courante : par exemple le bord de la trace lumineuse que fait une lampe à abat-jour ou une lampe de poche sur un mur est une conique.
 

Ombre elliptique

Ombre hyperbolique

Un cercle vu en perspective est une conique ; c'est une ellipse, une parabole ou une hyperbole suivant que l'observateur est à l'extérieur, sur ou à l'intérieur du cercle.
 

Un observateur situé au point (0, - d, h) regarde le cercle trigonométrique : quand il se rapproche du cercle, il voit d'abord une ellipse de grand axe parallèle à Ox , puis un cercle (cas d2 = h2 + 1), puis une ellipse de grand axe parallèle à Oy, puis une portion de parabole (cas d = 1) , et enfin une portion d' hyperbole.

 

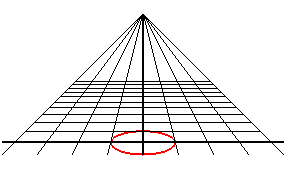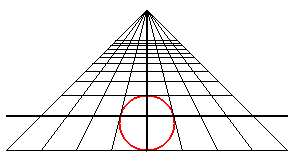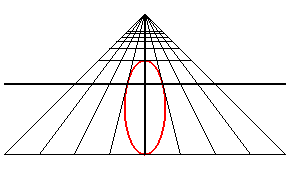
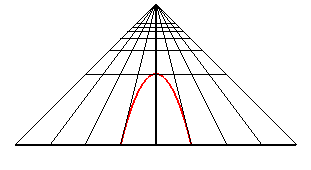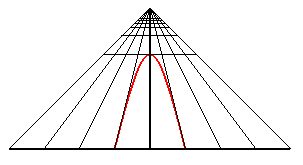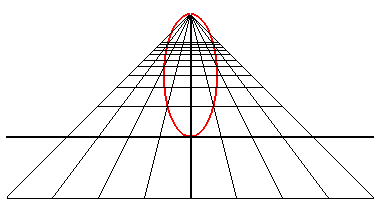Inversement, un observateur qui regarde la parabole y = x² voit, lui, une ellipse !

 

Dans ce théatre circulaire, les perspectives des gradins pour un spectateur situé sur l'un d'eux, sont des paraboles.

En fait, d'un point de vue projectif, il n'existe qu'une seule conique, en ce sens que les coniques sont toutes images entre elles par homographie.
 

La trajectoire d'une particule soumise à une force centrée en F proportionnelle à 1/MF² est une conique de foyer F :

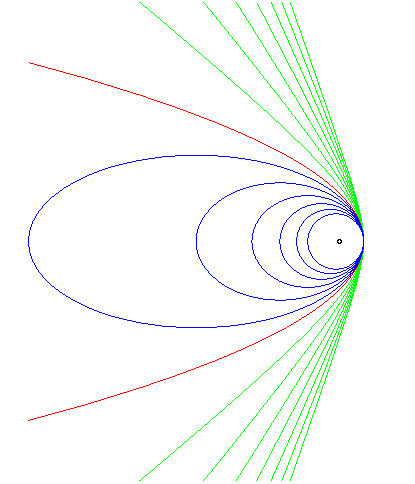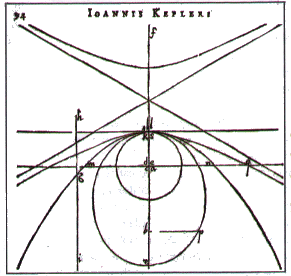
La même figure de la main de kepler

La trajectoire d'un bateau B se mouvant dans un courant de vitesse constante e.v, avec une vitesse constante v de sorte que son axe est constamment perpendiculaire à la droite BP, où P est un phare fixe est une conique de foyer P, d'excentricité e et d'axe focal parallèle au courant : dans un repère où Px est parallèle au courant. C'est donc une ellipse si la vitesse du bateau est supérieure à celle du courant, une parabole si elle lui est égale, une hyperbole si elle lui est inférieure. Le mouvement est en fait à accélération centrale en 1/ BP², exactement comme pour la particule ci-dessus.
(dans la même veine, voir la courbe du nageur).
 

Lorsque deux ondes circulaires issues de F et F' se rencontrent,  l'amplitude est proportionnelle à la différence des distances à F et F', et la phase est propoprtionnelle à la somme de ces distances : d'où ces figures d'interférence, formées d'un réseau orthogonal d'ellipses et d'hyperboles :

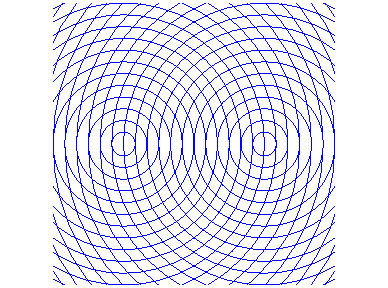
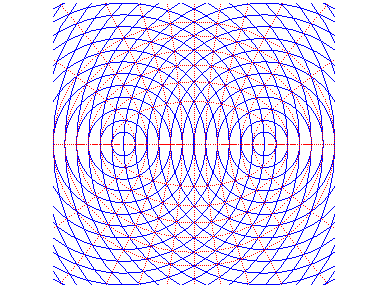
Les inverses de coniques sont les cubiques circulaires rationnelles lorsque le centre d'inversion est sur la conique, les quartiques bicirculaires rationnelles sinon.

Voir aussi les roulettes de Delaunay.

Sur les coniques, voir absolument aussi : www.ac-grenoble.fr/disciplines/spc/genevieve_tulloue/file/gtulloue/Coniques/Index_coniques.html
 
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2001