Courbe d'équidistance

COURBE D'ÉQUIDISTANCE, ENSEMBLE DE SYMÉTRIE, SQUELETTE
Equidistance curve, symmetry set, skeletton, Äquidistanzkurve, Symmetriemenge, Skelett

Autres noms : (courbe) médiatrice, courbe centrale, axe médian.
Voir capes 1986 pour la notion de ligne de partage.
Articles wikipedia : squelettisation, axe médian.
Programme maple pour le squelette d'un polygone convexe

Obtention de l'équation de l'équidistante : éliminer

entre

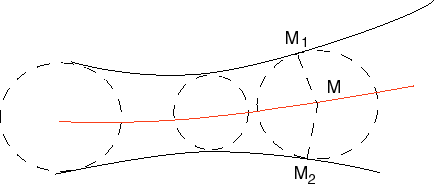
La courbe d'équidistance de deux courbes et est le lieu des points M situés sur une normale en M₁ à et sur une normale en M₂ à avec MM₁ =MM₂ . C'est donc aussi le lieu des centres des cercles tangents aux deux courbes.
Les courbes et sont donc symétriques par rapport à l'équidistante.

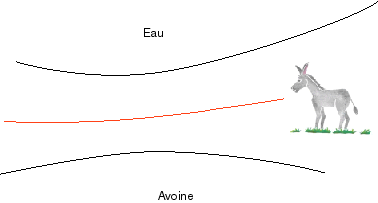
La courbe d'équidistance est la courbe d'indécision de l'âne de Buridan !

Exemples :
    - deux courbes parallèles ont pour courbe d'équidistance une autre courbe parallèle.
    - deux courbes symétriques par rapport à une droite ont une portion de cette droite comme courbe d'équidistance (par exemple, la courbe d'équidistance de deux droites sécantes est formée des deux bissectrices).
    - L'enveloppe d'une famille de cercles a pour équidistante avec elle-même le lieu du centre des cercles.
    - la courbe d'équidistance d'une courbe et d'un point est la courbe isotèle de cette courbe par rapport à ce point.
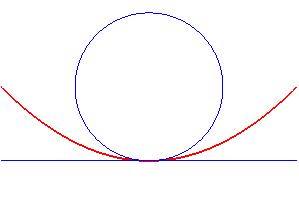
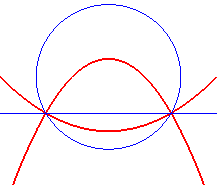
    - la courbe d'équidistance d'un cercle et d'une droite est formée d'une ou deux paraboles ; si le cercle est de centre F et de rayon R, et la droite notée D, la courbe d'équidistance est définie par où H est le projeté de M sur D. La, ou les paraboles sont de foyer F et de directrice parallèle à D.

Divers cas : cercle disjoint de la droite, tangent, ou sécant à la droite.

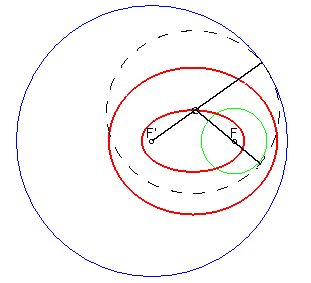
- la courbe d'équidistance de 2 cercles est formée de deux coniques bifocales ; si les cercles sont respectivement de (centre, rayon) : (F,R) et (F',R'), la courbe d'équidistance est définie par ; et dans l'espace, ces deux coniques sont des focales des deux cyclides de Dupin ayant les deux cercles pour cercles directeurs).
Ces deux coniques sont...

...deux ellipses lorsque les cercles sont intérieurs l'un à l'autre : ...une ellipse et une droite lorsque les cercles sont tangents intérieurement :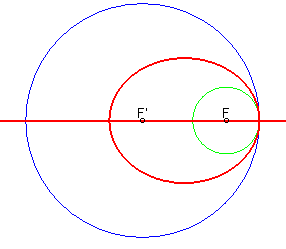

...une ellipse et une hyperbole lorsque les cercles sont sécants : 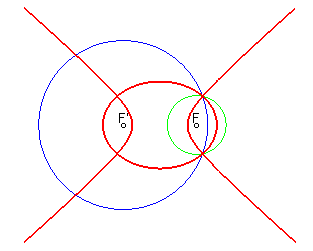...une ellipse et une hyperbole lorsque les cercles sont tangents extérieurement :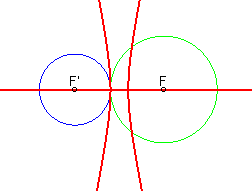

...deux hyperboles lorque les cercles sont extérieurs l'un à l'autre : 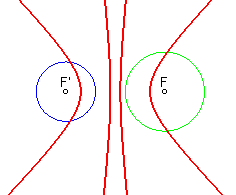Ci-contre, la courbe d'équidistance entre une droite et une parabole.
Courbe algébrique de degré 6.

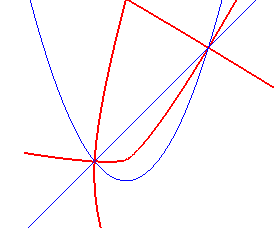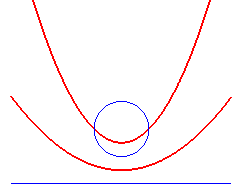
La courbe d'équidistance entre la néphroïde et le segment joignant les rebroussements est un cercle.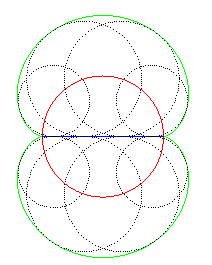

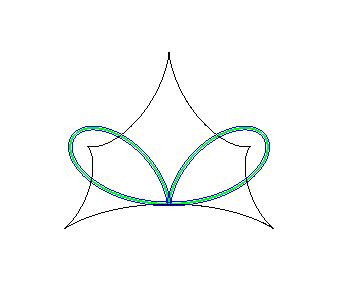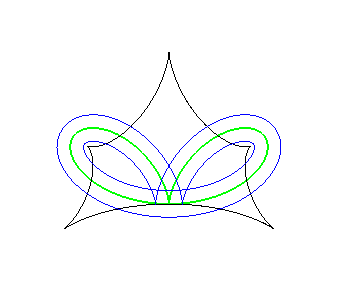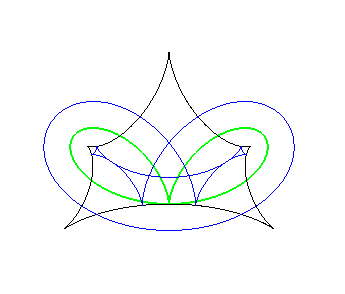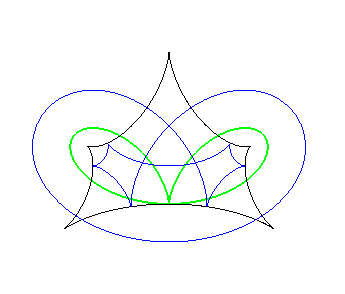
On peut considérer les cas où les deux courbes ne font qu'une. La courbe d'équidistance, qui prend alors le nom d'ensemble de symétrie, est le lieu des centres des cercles bitangents (ou multitangents) à la courbe, et donc aussi le lieu des points où les courbes parallèles se recoupent elles-même.

Exemples (courbes de départ en vert, courbes parallèles en bleu, squelette en rouge, développée en noir).

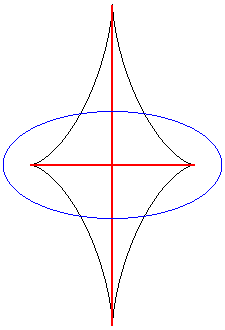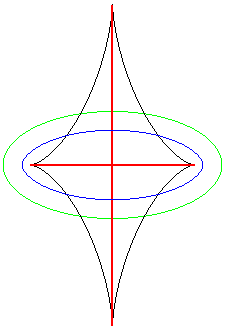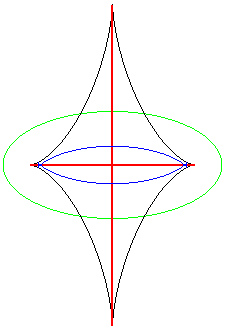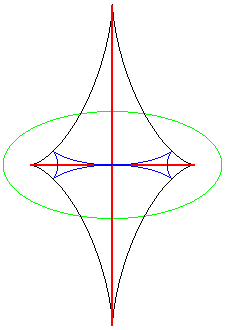
L'ensemble de symétrie d'une ellipse est formé des segments joignant 2 points de rebroussement de sa développée, se réduisant au centre dans le cas du cercle.
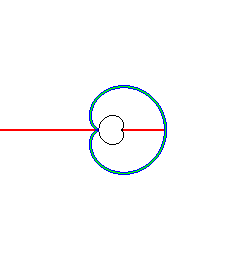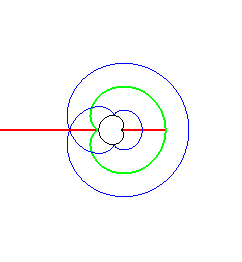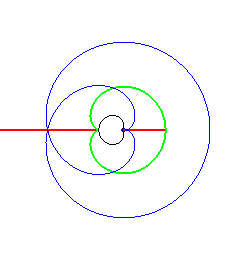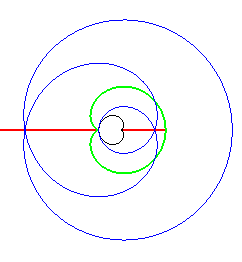
On voit bien sur cette animation que la courbe d'équidistance est le lieu des points doubles des courbes parallèles (des toroïdes), la développée étant le lieu des points de rebroussement. Ensemble de symétrie d'une cardioïde, lieu des points doubles des courbes parallèles. Ensemble de symétrie d'un bifolium (à imaginer, en regardant le lieu des points doubles des parallèles...)

L'ensemble de symétrie de l'enveloppe d'une famille de cercles est le lieu des centres (mais attention, certains cercles peuvent avoir un contact imaginaire avec la courbe : leur centre ne sera pas compté dans le squelette réel) ; par exemple, l'ensemble de symétrie d'une courbe anallagmatique est sa déférente.

Comme pour les courbes parallèles (cf. les lignes de distance), une notion voisine de celle de courbe d'équidistance est celle de courbe médiatrice de deux parties du plan, ensemble des points situés à égale distance de ces deux parties (la distance à une partie étant la borne inférieure des distances à un point de cette partie) ; lorsque les parties sont des courbes, la courbe médiatrice est en général incluse dans la courbe d'équidistance.
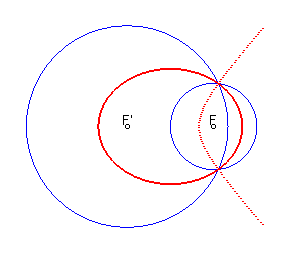
Voici par exemple la courbe médiatrice de deux cercles sécants, toujours formée d'une ellipse, mais dont l'hyperbole ne comporte plus qu'une branche :

Une généralisation est la notion de ligne de partage, où les distances ne sont plus égales, mais dans un rapport donné. Par exemple, les cercles d'Apollonius sont les lignes de partage de deux points, les coniques sont les lignes de partage d'une droite et d'un point, les ovales de Descartes, les lignes de partage de deux cercles.

Lignes de partage de deux cercles, définies par

.
En vert pour k > 1, en bleu pour 0 < k < 1 (ovales de Descartes), en rouge pour k = 1 (branche d'hyperbole, médiatrice des deux cercles).

La notion voisine de l'ensemble de symétrie est celle de squelette d'une partie compacte X du plan, qui est l'adhérence de l'ensemble des points M de cette partie, tels que la distance de M à la frontière de la partie est atteint en deux points distincts ; c'est aussi l'adhérence de l'ensemble des centres des disques maximaux inclus dans la partie (un disque maximal étant un disque qui n'est strictement inclus dans aucun autre).

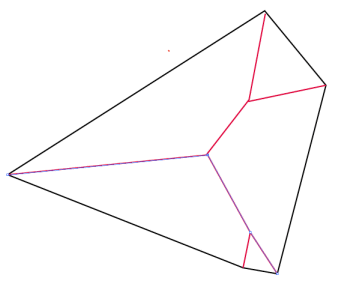
Par exemple, le squelette d'un triangle plein est formé des bissectrices intérieures, limitées aux sommets et au centre du cercle inscrit.

Pour un polygone convexe plein, le squelette est formé de portions de bissectrices de couples de côtés, limitant les "zones d'attraction" de chaque côté (lieux des points plus proches du côté considéré que des autres).
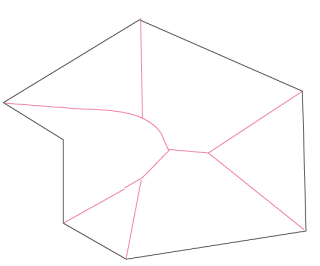
Dans le cas non convexe, le squelette comporte des portions de paraboles.

Pour une frontière C¹ par morceaux, le squelette est un arbre dont les extrémités sont les points anguleux sortants ou les centres de courbure aux sommets sortants de la frontière.
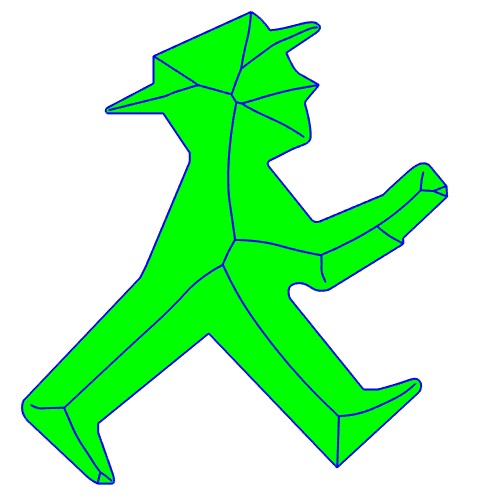
Image de gauche : arc de parabole en bleu, développée de l'arc symétrique en rouge, symétrique de l'arc bleu par rapport à l'arc rouge en vert ; l'arc rouge est donc le squelette de la réunion des arcs verts et bleu.
Image de droite réalisée par Robert March à partir de L'ampelmännchen berlinois.

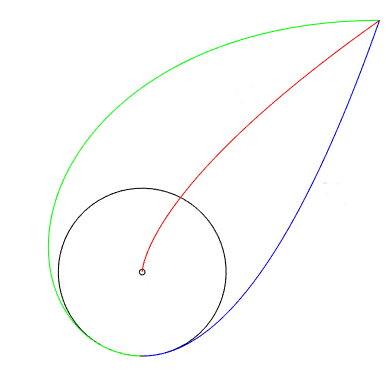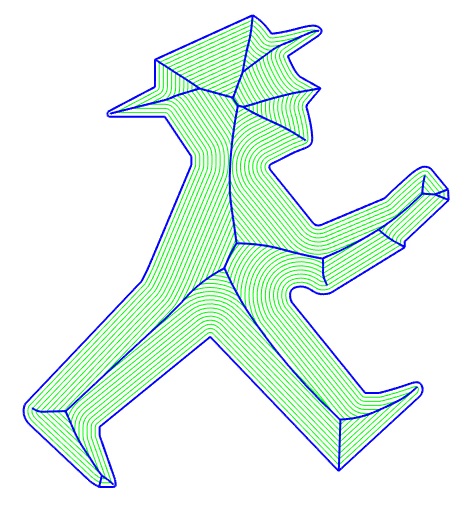Au sujet des squelettes, voir aussi les tas de sable, dont la crête se projette sur le squelette.

On peut étendre la notion au cas où X est une partie quelconque ; par exemple, si X est le complémentaire d'une partie finie Y, le squelette est formé des frontières des cellules de Voronoï associées aux points de cette partie.

Comparer avec la courbe médiane de deux courbes.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres

...deux ellipses lorsque les cercles sont intérieurs l'un à l'autre :		...une ellipse et une droite lorsque les cercles sont tangents intérieurement :
...une ellipse et une hyperbole lorsque les cercles sont sécants :		...une ellipse et une hyperbole lorsque les cercles sont tangents extérieurement :
...deux hyperboles lorque les cercles sont extérieurs l'un à l'autre :		Ci-contre, la courbe d'équidistance entre une droite et une parabole. Courbe algébrique de degré 6.

L'ensemble de symétrie d'une ellipse est formé des segments joignant 2 points de rebroussement de sa développée, se réduisant au centre dans le cas du cercle. On voit bien sur cette animation que la courbe d'équidistance est le lieu des points doubles des courbes parallèles (des toroïdes), la développée étant le lieu des points de rebroussement.	Ensemble de symétrie d'une cardioïde, lieu des points doubles des courbes parallèles.	Ensemble de symétrie d'un bifolium (à imaginer, en regardant le lieu des points doubles des parallèles...)