Notion étudiée par Mannheim en 1862. Anallagmatique signifie mot à mot : sans changement (du grec allagma "changement").

 

Equation polaire générale :  avec .

Une courbe est dite anallagmatique si elle est globalement invariante par inversion.

Toute courbe anallagmatique peut être générée comme cyclique, c'est-à dire comme enveloppe de cercles orthogonaux au cercle d'inversion (dans le cas d'une puissance positive), dont les centres décrivent l'une des déférentes de la courbe (au pluriel, car il peut y avoir en effet plusieurs générations de ce type) :

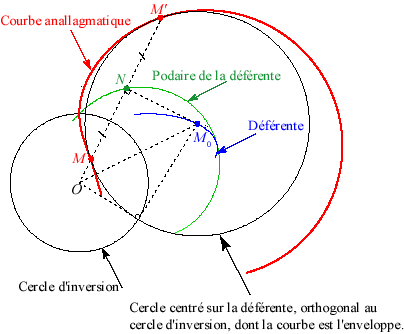
Dans le cas algébrique, elle est alors toujours circulaire.

Exemples de courbes anallagmatiques :
    - la droite (par rapport à l'un de ses points)
    - le cercle
    - les strophoïdes (le cercle d’inversion est centré au foyer (sur la boucle) et passe par le point double, la déférente est une parabole passant par le point double).
    - plus généralement toute cubique circulaire (le pôle d'inversion est le point de la cubique où la tangente est parallèle à l'asymptote réelle)
    - les limaçons de Pascal (par rapport au point d'abscisse   de Ox).
    - les ovales de Cassini et de Descartes.
    - plus généralement les quartiques bicirculaires et les quartiques circulaires à point double.
    - les spirales anallagmatiques.
 
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Jacques MANDONNET 2013