Équation cartésienne réduite :  (avec (0,1,0) comme point à l'infini, soit une direction asymptotique verticale).

Les cubiques circulaires sont les cubiques passant par les points cycliques ; on démontre que ce sont les cycliques dont la déférente est une parabole, autrement dit ce sont les enveloppes de cercles dont le centre décrit une parabole, et tels qu'un point fixe (le pôle) ait une puissance constante par rapport à ces cercles (c'est-à dire que ces cercles coupent orthogonalement ou pseudo-orthogonalement un cercle fixe, le cercle directeur).
Elle sont rationnelles ssi cette puissance est nulle.

Une cubique circulaire est obtenue par 4 définitions de ce type dans le cas général. Elle en perd une si elle possède un axe de symétrie. Indépendamment, elle en perd 2 ou 3 lorsqu’elle est rationnelle (selon le cas de point singulier).
Les pôles sont les points de la courbe où la tangente est parallèle à l’asymptote.

Exemples :
    - l'hyperbole cubique circulaire  est enveloppe des cercles  avec  ; la déférente est  et le cercle directeur .

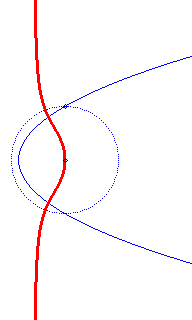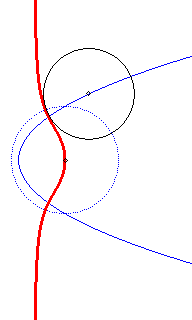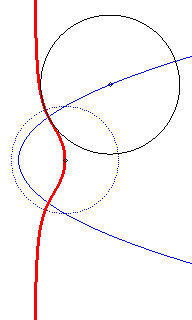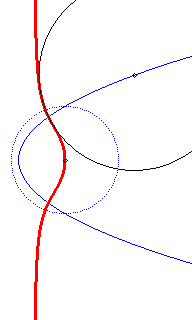Cercle directeur en pointillé ; les cercles ont au début un contact imaginaire avec la cubique.

© Robert FERRÉOL, Jacques MANDONNET 2001