Cyclique

CYCLIQUE
Cyclic curve, Zyklische Kurve

Du grec Kuklos : cercle, roue.

Équation polaire: où est la podaire de la déférente, O le centre d'inversion et p la puissance.
Condition de réalité des points de la cyclique : .

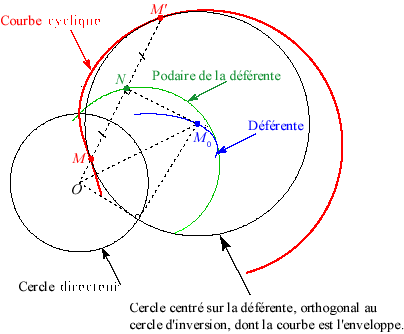
La (courbe) cyclique associée à une courbe (la déférente), un centre O et une puissance p est l'enveloppe des cercles (C) dont le centre décrit et tels que O ait une puissance constante p par rapport à ces cercles.
L'on désigne alors par cercle directeur (C₀) (ou cercle d'inversion) le cercle de centre O et de rayon ; la condition de puissance constante signifie :
- dans le cas où p est > 0, que (C) reste orthogonal au cercle directeur.
- dans le cas où p est nul, que (C) passe par O.
- dans le cas où p est < 0, que (C) reste "pseudo-orthogonal" au cercle directeur, autrement dit qu'il le coupe en deux points diamétralement opposés.

Dans le cas où p > 0, le cercle (C) n'est réel que pour les points de la déférente situés en dehors du cercle directeur ; pour les points intérieurs, la portion de cyclique obtenue n'a que des points imaginaires.

Considérons le projeté N de O sur la tangente (T₀) à en (M₀) (N décrit donc la podaire de par rapport à O).
Les deux points caractéristiques M et M' du cercle (C) centré en (M₀) sont les points d'intersection de (C) avec (ON). Ils sont alors définis par

et sont donc réels ssi ON²³ p ; on en déduit l'équation polaire donnée en en-tête.

Lorsque p est différent de 0, la cyclique est donc anallagmatique de centre d'inversion O et de puissance p, et réciproquement toute courbe anallagmatique possède autant de générations cycliques qu'elle possède de centres d'inversion.

Lorsque p est nul, il n'y a plus qu'un point caractéristique M tel que N est le milieu de [OM] et la cyclique n'est autre que l'orthotomique de par rapport à O.

Les cycliques de déférente une parabole sont les cubiques circulaires (rationnelles si p = 0) et les cycliques de déférente une conique à centre sont les quartiques bicirculaires (rationnelles si p = 0).

L'analogue de la notion de cyclique pour les surfaces est celle de cyclide.

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres