C'est aussi l'enveloppe des cercles centrés sur (G0) et passant par O ; voir à anallagmatique.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE ORTHOTOMIQUE
Orthotomic curve, Orthotomische Kurve
| Notion étudiée par Quételet en 1822
(?)
Du grec orthos "droit" et tomê "coupure, section". Autre nom : podoïde. |
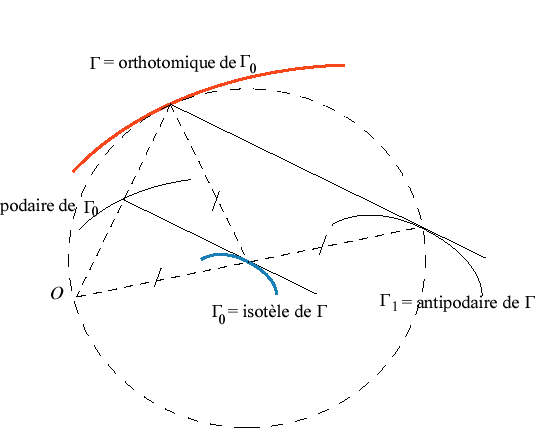
| La courbe orthotomique d'une courbe plane (G0)
par rapport à un point O est le lieu des symétriques
de O par rapport aux tangentes à la courbe (G0).
C'est donc l'image de la podaire
de (G0) par
rapport à O dans une homothétie de centre O
et de rapport 2.
C'est aussi l'enveloppe des cercles centrés sur (G0) et passant par O ; voir à anallagmatique. |
|
Sa développée est la caustique par réflexion de (G0) pour une source lumineuse placée en O : la courbe orthotomique est donc un cas particulier d'anticaustique (ou caustique secondaire).
On peut aussi considérer la courbe orthotomique comme une roulette : lorsqu'on fait rouler sans glisser la courbe (G0) sur elle-même de façon à ce que les deux courbes soient symétriques par rapport à leur tangente commune, la trace du point O du plan mobile dans le plan fixe est la courbe orthotomique (c'est pourquoi, par exemple, la cardioïde est à la fois podaire de cercle par rapport à l'un de ses points et épicycloïde. Voir aussi la construction de la cissoïde droite comme roulette).
Exemples :
- l’orthotomique d’une conique
à centre par rapport à l’un de ses foyers est le cercle directeur
centré en l’autre foyer ;
- l’orthotomique d’une parabole
par rapport à son foyer est sa directrice.
Pour des exemples exhaustifs, voir à podaire.
La courbe dont une courbe donnée est l'orthotomique
est la courbe isotèle de
la courbe de départ.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL, Jacques MANDONNET 2004