COURBE ORTHOPTIQUE
Orthoptic
curve, orthoptische Kurve

| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
COURBE ORTHOPTIQUE
Orthoptic
curve, orthoptische Kurve

| Du grec orthos "droit" et optikos "relatif
à la vue".
Appellation donnée par Taylor en 1884. |
| Une méthode pour obtenir l'équation de l'orthoptique
de la courbe f(x,y)=0 : éliminer x1,y1,x2,y2 entre les 5 équations
: f(x1,y1)=0, f(x2,y2)=0, p(x1,y1)*(x-x1)+q(x1,y1)*(y-y1)=0, p(x2,y2)*(x-x2)+q(x2,y2)*(y-y2)=0,
et (x-x1)*(x-x2)+(y-y1)*(y-y2)=0 (p et q étant les deux dérivées
partielles de f).
Une méthode pour obtenir l'équation de l'orthoptique de la courbe x=f(t),y=g(t) : éliminer t et u entre les 3 équations : g'(t)*(x-f(t))-f'(t)*(y-g(t))=0, g'(u)*(x-f(u))-f'(u)*(y-g(u))=0, et (x-f(t))*(x-f(u)+(y-g(t))*(y-g(u))=0. |
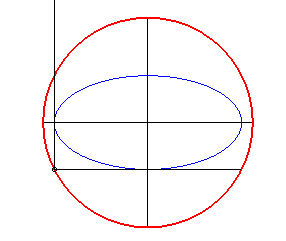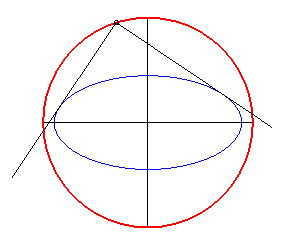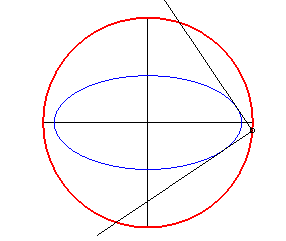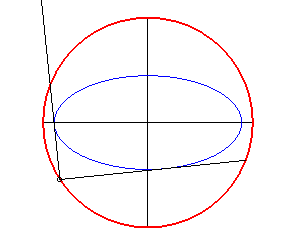
La (courbe) orthoptique d'une courbe est le lieu des points d'où l'on peut mener deux tangentes à la courbe perpendiculaires entre elles, autrement dit le lieu des points d'où l'on "voit" la courbe sous un angle droit ; c'est donc un cas particulier de courbe isoptique.
Exemples :
- L’orthoptique de la parabole
est sa directrice.
- L’orthoptique d’une conique à
centre d'excentricité inférieure à
est un cercle appelé cercle orthoptique ou cercle de Monge. Pour
l’ellipse, c’est le cercle de centre O et de rayon
(circonscrit à son rectangle). Pour l’hyperbole, c’est le cercle
de centre O et de rayon
.
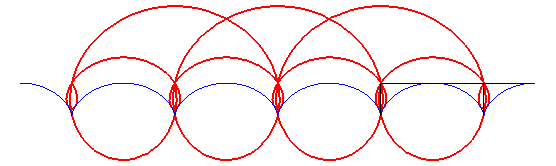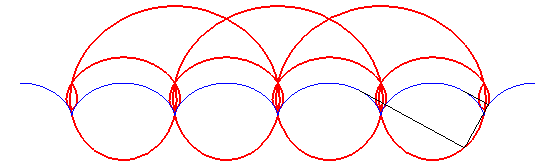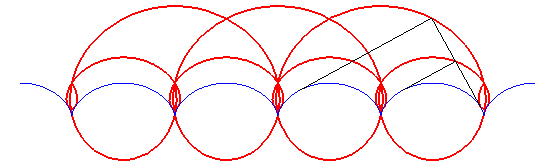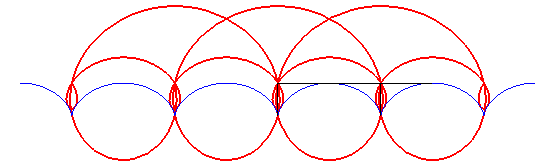
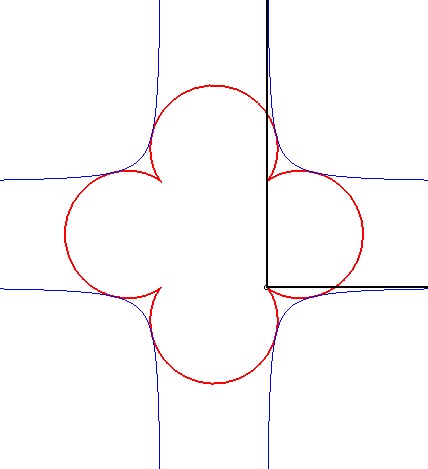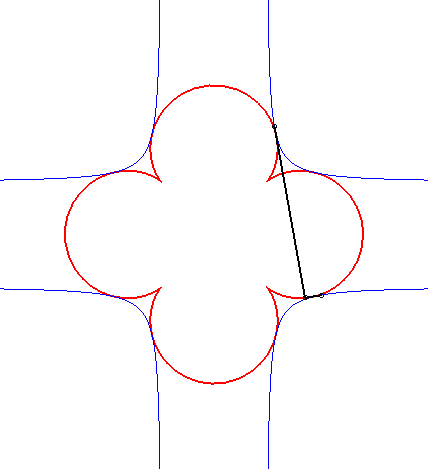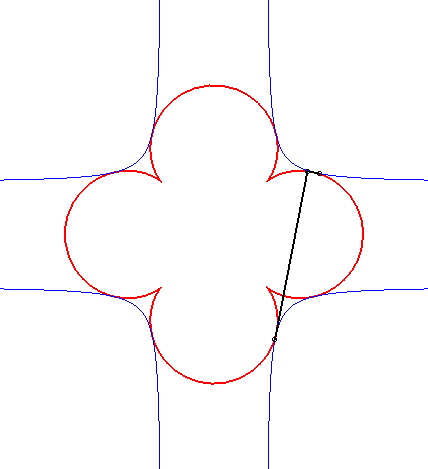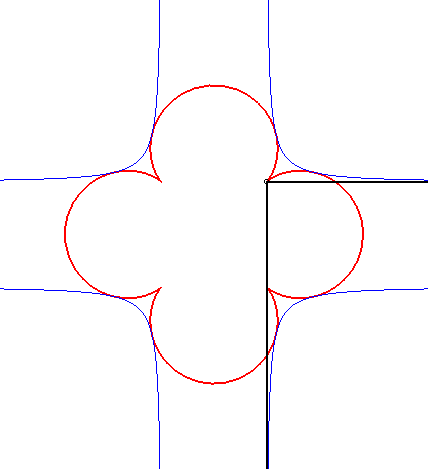
- L’orthoptique de la cardioïde
est la réunion d'un cercle et d'un limaçon
de Pascal à boucle avec
(voir l'animation ci-dessus).
- L’orthoptique de la deltoïde
est son cercle inscrit.
 |
 |
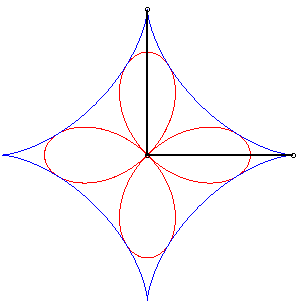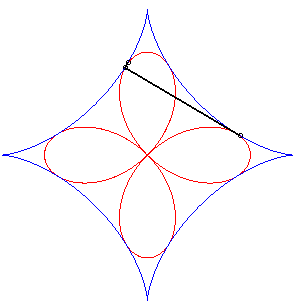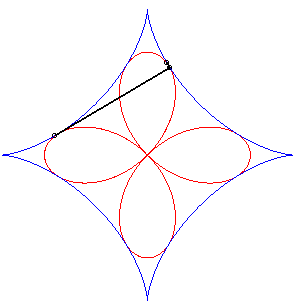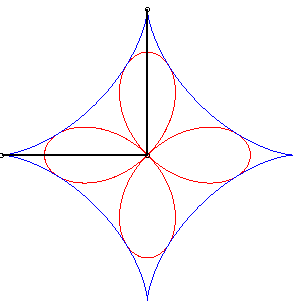
| - l'ortoptique de l'astroïde est un quadrifolium. | - l'orthoptique de la cruciforme est une belle courbe à 4 rebroussements (voir à tétracuspide). |
- plus généralement, l'orthoptique d'une courbe trochoïdale est une réunion de courbes trochoïdales.
- l'orthoptique d'une spirale logarithmique est une spirale logarithmique.
- la tractrice est l'orthoptique d'une réunion de deux logarithmiques.
- l'orthoptique de la croix de Malte est la cornoïde.
- la podaire d'une courbe peut être considérée comme l'orthoptique de la réunion de cette courbe et d'un point.
Autres exemples Broc comp p. 134.
La courbe orthoptique de la développée d'une courbe est le lieu des points d'où l'on peut mener deux normales à la courbe de départ, perpendiculaires entre elles.
Une notion voisine, portant le même nom, est celle d'orthoptique d'une partie X du plan : lieu des sommets des secteurs angulaires droits circonscrivant X (c'est-à-dire contenant X, et dont les deux côtés rencontrent X). L'orthoptique de la cardioïde dessinée en haut de cette page ne sera alors plus formée que de la partie externe des courbes rouges.
Voir la notion de surface
orthoptique.
| courbe suivante | courbe précédente | courbes 2D | courbes 3D | surfaces | fractals | polyèdres |
© Robert FERRÉOL 2013