Du grec tetra "quatre" et du latin cuspis "pointe". Nom donné par Bellavitis en 1854. Autre nom : quadricuspide (plus logique étymologiquement...).

Les tétracuspides sont les courbes fermées à 4 points de rebroussements.

Voici des exemples où les 4 points de rebroussements pointent vers l'extérieur (tétracuspide saillante) :
 
 

Le plus simple est l'astroïde, ainsi que ses déformations affines :

 

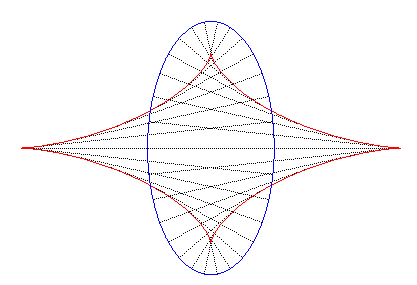
La développée de l'ellipse :  avec  , qui est un cas particulier d'astroïde dilatée.

Un autre exemple, qui contient aussi l'astroïde comme cas particulier est donné par la

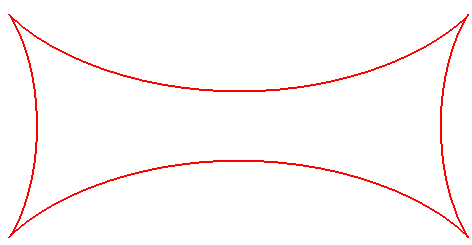
Problème posé par Merlieux en 1842, résolu en 1847 par Joachimsthal.

La tétracuspide de Joachimsthal est l'enveloppe de la droite contenant un segment de longueur constante a dont les extrémités se déplacent sur deux droites sécantes quelconques.
 
 

Les deux droites sécantes étant les droites faisant un angle  avec Ox, et choisissant , on obtient : Paramétrisation cartésienne : , u et v étant reliés par la relation .  Courbe sextique rationnelle.

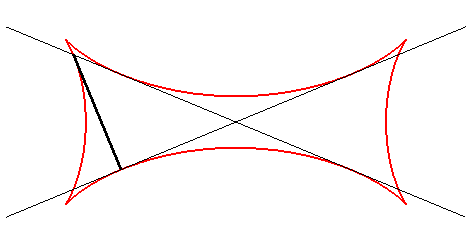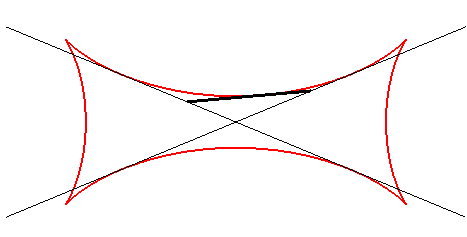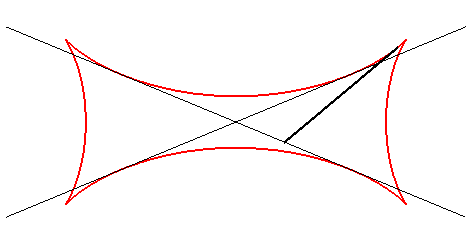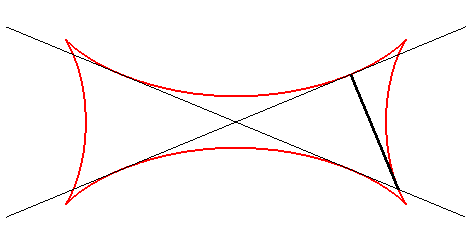
Les points de la droite mobile décrivent, eux, des ellipses.

Autres tétracuspides saillantes :
    - la croix de Malte.
    - certaines toroïdes
    - certaines reptoires d'ellipses
 

Voici des exemples où les 4 points de rebroussements pointent vers l'intérieur (tétracuspide rentrante) :
 
 

L'épicycloïde à 4 rebroussements :
La famille des courbes de paramétrisation :  pour n entier impair . Ci-contre, le cas n = 5 :
Il se trouve que le cas n = 3 s'obtient comme orthoptique de la cruciforme :
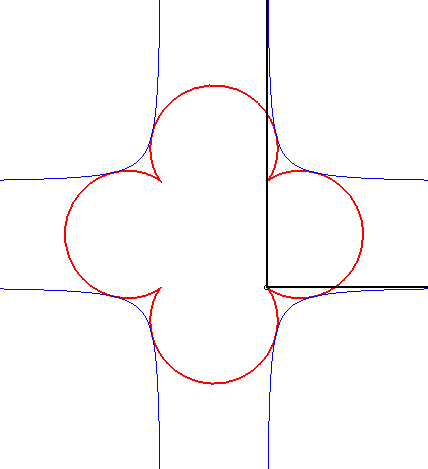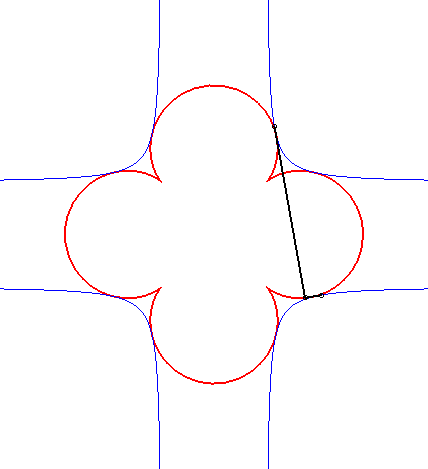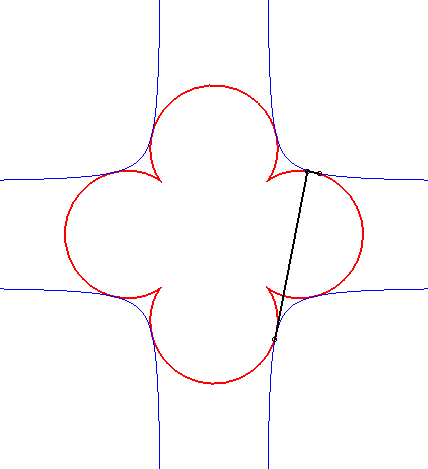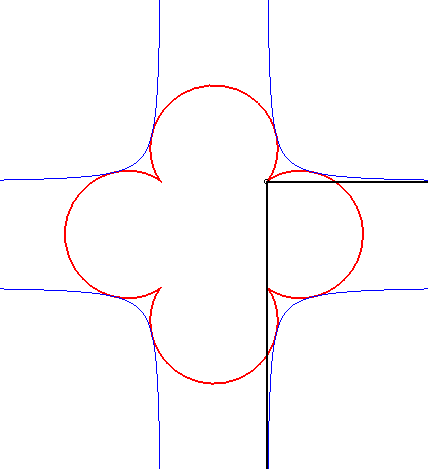Les courbes précédentes ont pour équation cartésienne  où   et sous cette forme, on peut prendre  quelconque entre 0 et 1. Ci-contre le cas = 1/2.

 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2015