Si la base est paramétrée par (M(t)) et la rampante paramétrée par (N(u)), la reptoire est paramétrée par (M(t)-N(u)), les paramètres u et t étant liés par la relation .

Lorsqu'une courbe mobile (la rampante) se déplace dans un mouvement de translation en restant tangente à une courbe fixe (la base), les courbes tracées par un point du plan de la courbe mobile sur le plan fixe sont appelées des reptoires.

Propriétés :
    1) la tangente à la reptoire est parallèle à la tangente commune au point de contact entre la base et la rampante.
    2) les diverses reptoires sont toutes translatées les unes des autres.
    3) si l'on échange la base et la rampante (en conservant leur orientation), les nouvelles reptoires sont image des anciennes par symétrie centrale.
    4) si l'on fait ramper la reptoire sur la base, les nouvelles reptoires sont des translatées de l'ancienne rampante.
    5) lorsqu'on fait ramper un cercle de rayon a sur une courbe, la reptoire du centre du cercle est l'une des 2 courbes parallèles à la distance a (donc idem si l'on fait ramper la courbe sur le cercle)
    5) si l'on se donne la reptoire et la rampante, on obtient la base comme enveloppe des diverses positions de la rampante.

Nota 1: la base ici définie est différente de la base au sens du mouvement plan sur plan, qui est, elle, ici, rejetée à l'infini.
Nota 2 : avec un langage plus moderne, les propriétés 2) et 3) peuvent s'exprimer sous la forme : si F₁, F₂ et F₃  sont trois arcs paramétrés de somme nulle et de dérivées deux à deux colinéaires, et {1,2,3}={i,j,k}  alors  si on fait ramper Fj  sur - Fi  la reptoire est Fk.
 

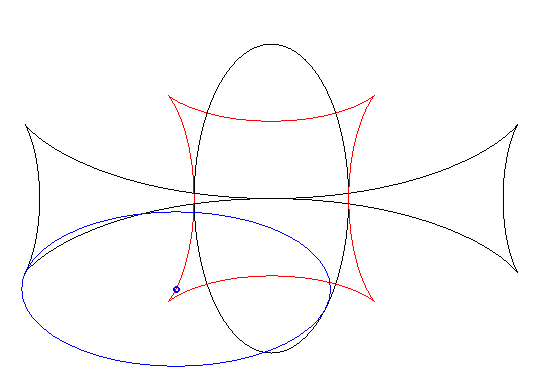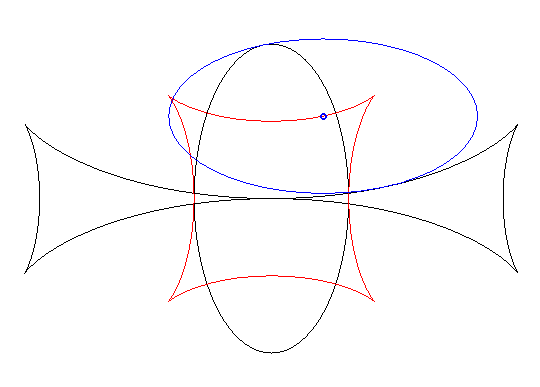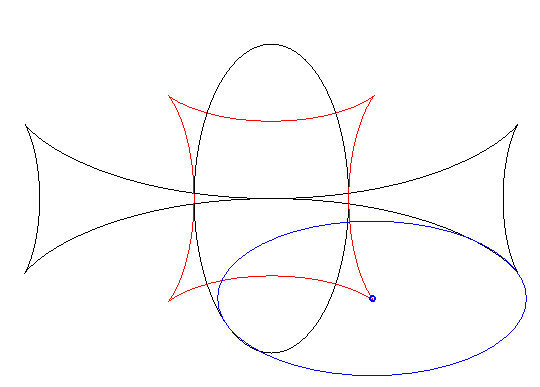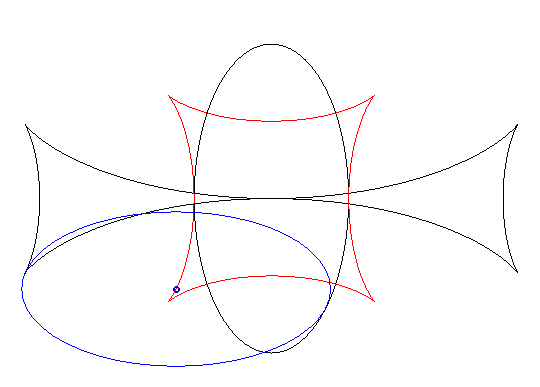
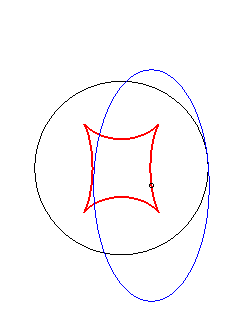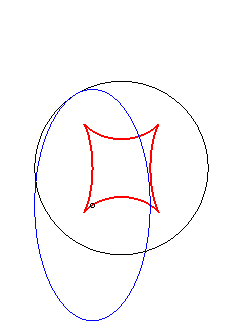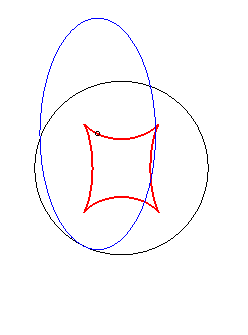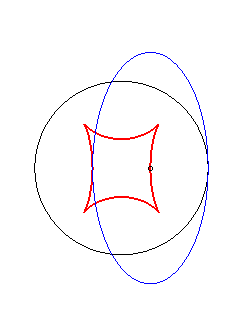
Exemple illustrant cette dernière propriété (base en noir, rampante en bleu et reptoire en rouge) :

,

Une ellipse (E) rampe sur un cercle (C) : on obtient une reptoire (R)	(C) rampe sur (E) : on obtient la même reptoire, qui est donc une courbe parallèle à l'ellipse (ou toroïde)	(R) rampe sur (C) : la reptoire est l'ellipse (E)
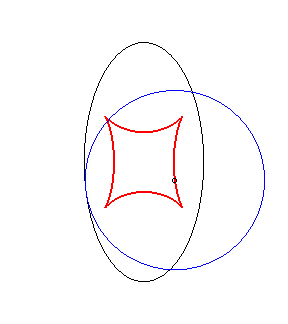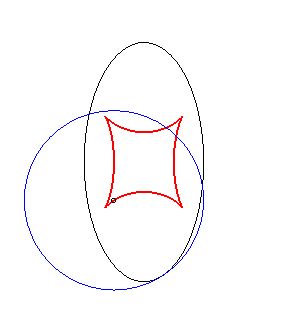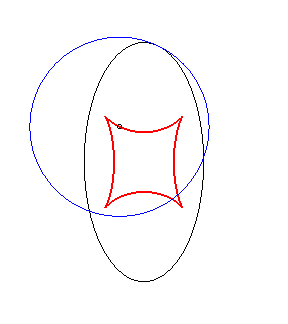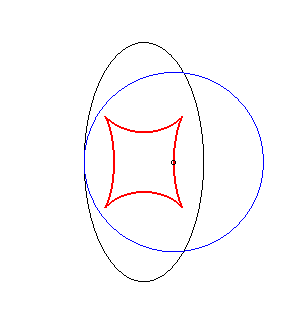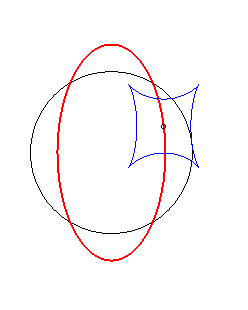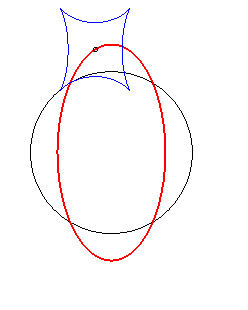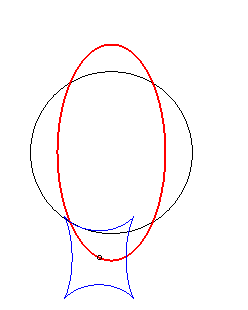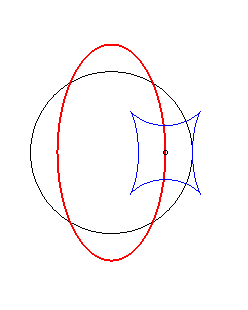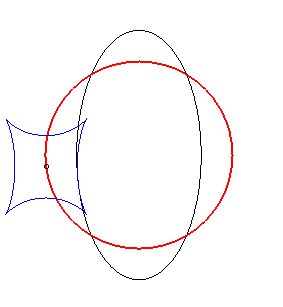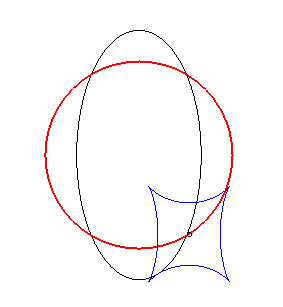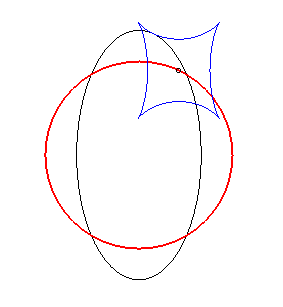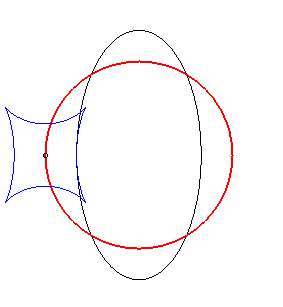
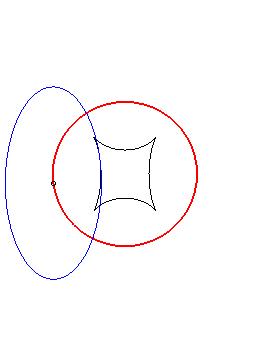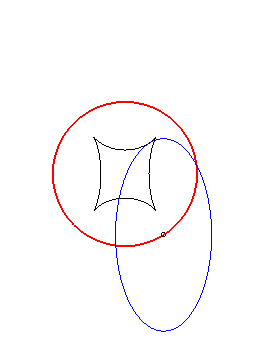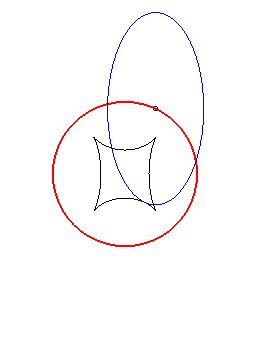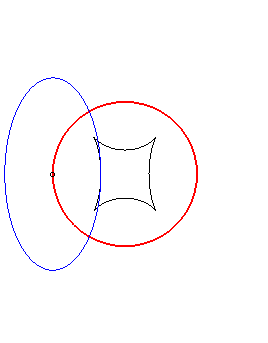
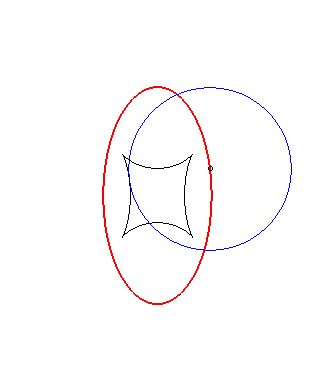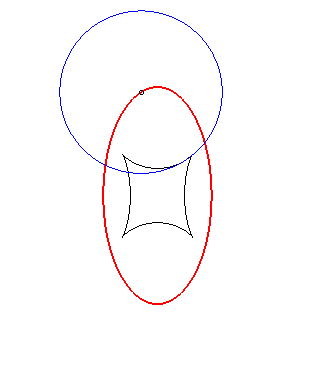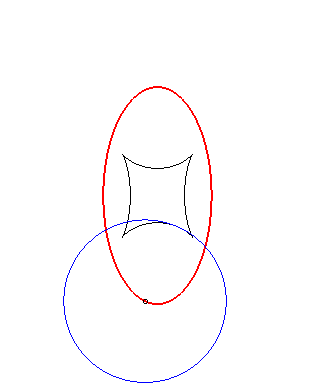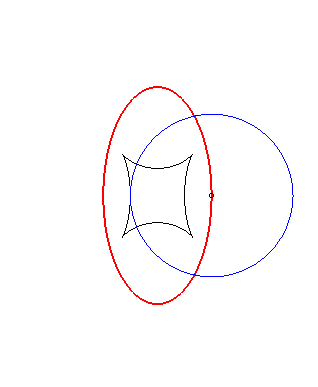
(R) rampe sur (E) : la reptoire est le cercle (C)	(E) rampe sur (R) : la reptoire est le cercle (C)	(C) rampe sur (R) : la reptoire est l'ellipse (E)

 

Lorsqu'on fait ramper une ellipse sur son image par une rotation d'angle droit, la reptoire est une courbe invariante par rotation d'angle droit ressemblant à l'astroïde (mais non rationnelle), de paramétrisation :  La rampante enveloppe une autre courbe (en pointillé ci-contre), ressemblant lorsque b = 2a à la croix de malte.

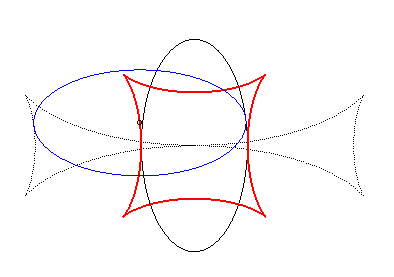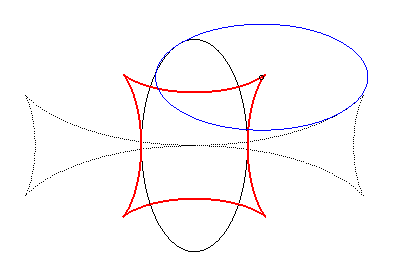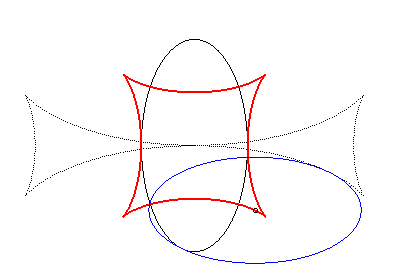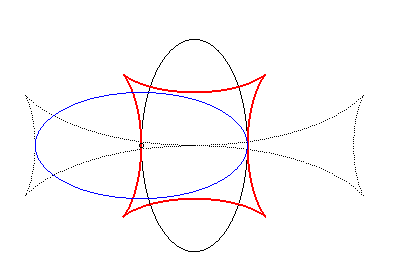Voir aussi les glissettes.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL , Alain ESCULIER 2008