Courbe tautochrone

COURBE TAUTOCHRONE
Tautochronous curve, Tautochrone Kurve

Courbe étudiée par Huygens en 1673 et Newton en 1687.
Du grec tauto "le même" et chronos "temps".

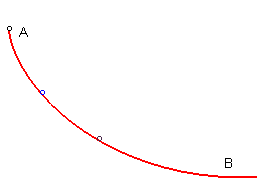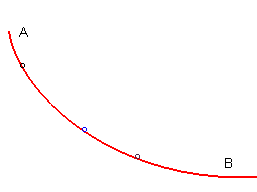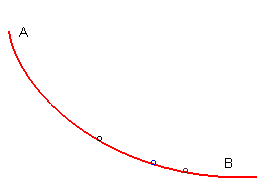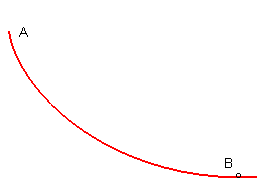
Une courbe joignant un point A à un point B situé plus bas est tautochrone si tout point matériel lâché sans vitesse initiale sur la courbe entre A et B arrive en B en un temps indépendant du point de départ.
La solution est une demi-arche de cycloïde.

Le problème ci-dessus a évidemment été résolu dans le cas d'un champ de pesanteur uniforme.
Pour le champ de pesanteur radial à l'intérieur de la terre, la solution serait une hypocycloïde.

Voir aussi brachistochrone et isochrone.

D'où que vous partiez, vous mettrez le même temps pour arriver en bas, mais vous n'y arriverez pas à la même vitesse !

courbe suivante courbe précédente courbes 2D courbes 3D surfaces fractals polyèdres