Propriété de la cycloïde découverte par Huygens en 1673.

La courbe isochrone de Huygens est la courbe telle qu'un point matériel se déplaçant sans frottement sur elle a un mouvement périodique dont la période est indépendante de la position initiale ; la solution est une arche de cycloïde dont les points de rebroussement sont situés vers le haut ; l'isochronie vient en fait de la tautochronie. La période du mouvement est  où L est la flèche de la cycloïde.

Le pendule cycloïdal de Huygens ci-dessous utilise cette propriété et le fait que la développée d'une cycloïde est une cycloïde égale. Son intérêt est d'avoir une période d'oscillation T =  indépendante de l'amplitude, contrairement au pendule libre dont seules les "petites" oscillations peuvent être considérées comme ayant la période T.

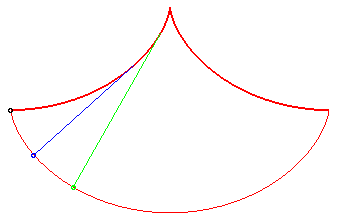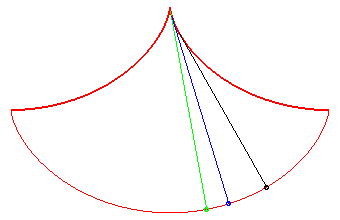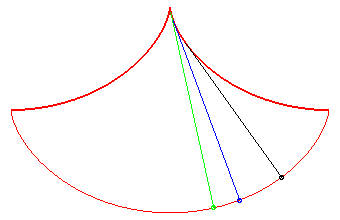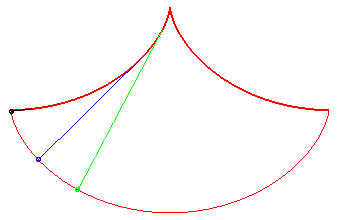
Dans ce problème de Huygens, tous les points atteignent le point le plus bas en même temps ; Galilée a posé le même problème, mais pour des points matériels se déplaçant sur des supports rectilignes : voir à courbe synchrone.
 

Voir aussi à isochrone de Leibniz et isochrone de Varignon pour un autre type d'isochronisme, et à synodale, brachistochrone et tautochrone.
 

courbe suivante

courbe précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL 2017